1) квадрат; 2) прямоугольник; 3) параллелограмм; 4) равнобочная трапеция
Объяснение:
Находим длины сторон четырёхугольника по формуле
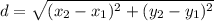
1) A(-2; 0), B(0; -2), C(2; 0), D(0; 2)
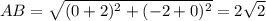
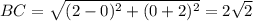
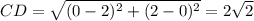
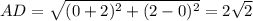
Четырёхугольник, у которого все стороны равны, является ромбом.
Найдём длины диагоналей ромба
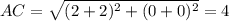
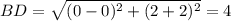
Ромб, диагонали которого равны, является квадратом.
АВСD - квадрат
2) A(-2; 1), B(2; -1), C(3; 1), D(-1; 3)
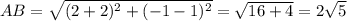

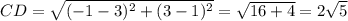
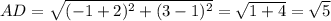
Четырёхугольник, у которого противоположные стороны попарно равны, является параллелограммом.
Найдём длины диагоналей параллелограмма
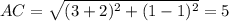
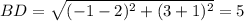
Параллелограмм, диагонали которого равны, является прямоугольником.
АВСD - прямоугольник
3) A(-2; 1), B(2; 2), C(1; 4), D(-3; 3)
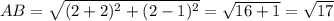
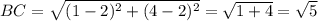
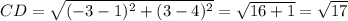
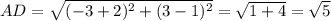
Четырёхугольник, у которого противоположные стороны попарно равны, является параллелограммом.
Найдём длины диагоналей параллелограмма
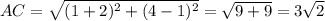
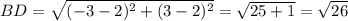
Диагонали параллелограмма имеют различную длину.
АВСD - параллелограмм
4) A(-2; -1), B(2; -1), C(1; 2), D(-1; 2)
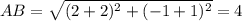
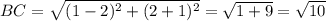
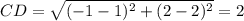
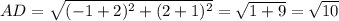
Уравнение прямой, содержащей сторону АВ у = -1, а уравнение прямой, содержащей сторону CD, у = 2. Следовательно АВ║ СD.
Запишем уравнение прямой, содержащей сторону ВС:

3x - 6 = -y - 1
y = -3x + 5
Запишем уравнение прямой, содержащей сторону AD:
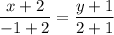
3x + 6 = y + 1
y = 3x + 5
Очевидно, что ВС ∦ AD
Четырёхугольник, у которого две противоположные стороны параллельны, а две другие не параллельны, является трапецией.
Видим, что боковые стороны трапеции ВC = AD
АВСD - равнобочная трапеция
1) квадрат; 2) прямоугольник; 3) параллелограмм; 4) равнобочная трапеция
Объяснение:
Находим длины сторон четырёхугольника по формуле
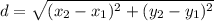
1) A(-2; 0), B(0; -2), C(2; 0), D(0; 2)
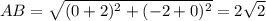
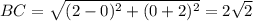
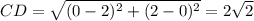
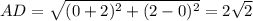
Четырёхугольник, у которого все стороны равны, является ромбом.
Найдём длины диагоналей ромба
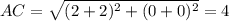
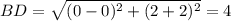
Ромб, диагонали которого равны, является квадратом.
АВСD - квадрат
2) A(-2; 1), B(2; -1), C(3; 1), D(-1; 3)
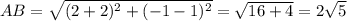

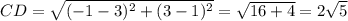
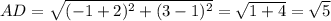
Четырёхугольник, у которого противоположные стороны попарно равны, является параллелограммом.
Найдём длины диагоналей параллелограмма
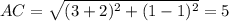
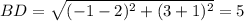
Параллелограмм, диагонали которого равны, является прямоугольником.
АВСD - прямоугольник
3) A(-2; 1), B(2; 2), C(1; 4), D(-3; 3)
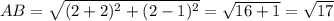
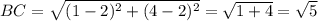
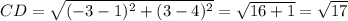
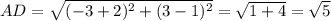
Четырёхугольник, у которого противоположные стороны попарно равны, является параллелограммом.
Найдём длины диагоналей параллелограмма
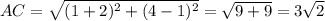
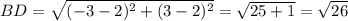
Диагонали параллелограмма имеют различную длину.
АВСD - параллелограмм
4) A(-2; -1), B(2; -1), C(1; 2), D(-1; 2)
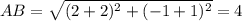
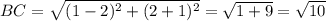
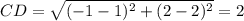
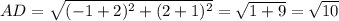
Уравнение прямой, содержащей сторону АВ у = -1, а уравнение прямой, содержащей сторону CD, у = 2. Следовательно АВ║ СD.
Запишем уравнение прямой, содержащей сторону ВС:

3x - 6 = -y - 1
y = -3x + 5
Запишем уравнение прямой, содержащей сторону AD:
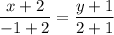
3x + 6 = y + 1
y = 3x + 5
Очевидно, что ВС ∦ AD
Четырёхугольник, у которого две противоположные стороны параллельны, а две другие не параллельны, является трапецией.
Видим, что боковые стороны трапеции ВC = AD
АВСD - равнобочная трапеция
Гордійко лох
Объяснение:
Хахахахахахаха