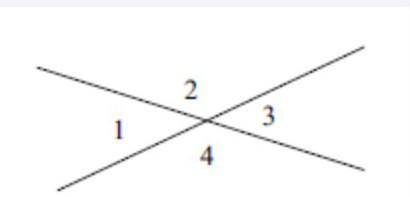
Решение, а) По условию Z2 + Z4 = 220°. Эти углы вертикальные, поэтому Z2 = Z4 = 110°.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°, откуда Z1 = 180° -- 110° = 70°.
Углы 3 и 1 вертикальные, поэтому Z3 = Z1 = 70°.
б) Углы 1 и 3, а также 2 и 4 вертикальные, поэтому Z3 = Zl, Z4 = = Z2. Подставив эти выражения в данное равенство, получим:
3(2Z1) = 2Z2,
или
3Z1 =Z2.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°. Из этих двух равенств находим Z1 и Z2: Z1 = 45°, Z2 = 135°.
Z3 = Z1, поэтому Z3 = 45°; Z4 = Z2, поэтому Z4 = 135°
в) По условию Z2 — Z1 = 30°. Эти углы смежные, следовательно, Zl + Z2 = 180°. Из этих двух равенств имеем: Z1 = 75°, Z2 = 105°.
Z3 = Z1, поэтому Z3 = 75°; Z4 = Z2, поэтому Z4 = 105°.
ответ, a) Zl = Z3 = 70°, Z2 = Z4 = 110°; б) Zl =Z3 = 45°, Z2 = = Z4 = 135°; в) Zl = Z3 = 75°, Z2 = Z4 = 105°.
а) a и KM могут быть параллельными либо скрещивающимися прямыми
б) a и KT могут быть только скрещивающими прямыми
Объяснение:
Если прямые a и KM параллельны, то расстояние между этими прямыми может быть любым и не зависит от расстояния между плоскостями.
То же самое касается и прямых a и KT.
Если одновременно все прямые параллельны, то при этом расстояние между плоскостями не определить.
Допустим теперь, что прямые а и KM - скрещивающиеся. Тогда по определению расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат. Отсюда получается, что расстояние между плоскостями α и β равно расстоянию между прямыми а и KM, т.е. 5.
При этом прямые a и KT будут параллельными.
Обратная ситуация невозможна, т.е. когда прямые a и KT являются скрещивающимися, а прямые а и KM параллельными, т.к. в таком случае расстояние между параллельными плоскостями равно расстоянию между любыми скрещивающимися прямыми, лежащими в этих плоскостях, т.е. расстоянию между прямыми a и KT, которое равно 8, из-за чего прямые а и KM не могут лежать в плоскостях, т.к. расстояние между ними меньше расстояния между плоскостями.
Вот ответ задачи по математике заранее не за что.