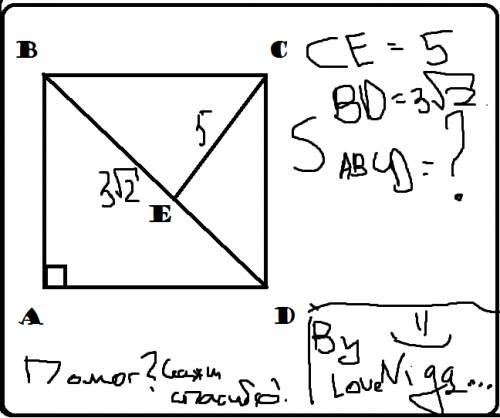
Из точки Е на ВС надо провести перпендикуляр. Пусть он пересекается с ВС в точке К. Тогда ВКЕ - равнобедренный прямоугольный треугольник, и его катеты ВК = ЕК = 3.
В прямоугольном треугольнике ЕКС катет ЕК = 3, гипотенуза ЕС = 5, то есть это "египетский" треугольник, его второй катет равен КС = 4.
Отсюда сторона квадрата ВС = 3 + 4 = 7, а площадь квадрата 7^2 = 49;
На самом деле, есть еще интересная возможность - если ЕD > BD. То есть точка E лежит на продолжении BD за точку B. В этом случае суть решения не меняется, но сторона квадрата ВС = 1, и площадь тоже 1.
Пусть SABC - прав. треуг. пирамида. Проведем SD перп ВС, SO перп АВС. АК перп SD. По условию АК = 3кор3, угол SDO = 60 гр.
Тогда из пр. треуг. AKD: AD = AK/sin 60 = 6 - высота правильного треуг. АВС.
OD = AD/3 = 2. Тогда из треуг. SOD высота боковой грани SD = 2/cos 60 = 4.
Сторона основания равна: ВС = AD/sin60 = 4кор3.
Теперь площадь бок пов-ти пирамиды равна:
Sбок = 3*(1/2)*ВС*SD = 24кор3.
ответ: 24кор3