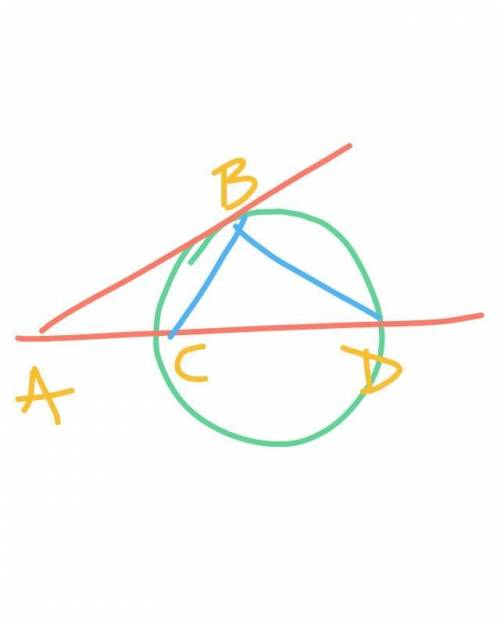
∠DAB = 30°
Объяснение:
Вписанный угол равен половине дуги, на которую он опирается, значит
∠BCD = 1/2 ∪DB = 1/2 · 100° = 50°
∠BDC = 1/2 ∪CB = 1/2 · 40° = 20°
Угол между касательной и хордой равен половине дуги, заключенной внутри этого угла, значит
∠АВС = 1/2 ∪СВ = 1/2 · 40° = 20°
∠BCD - внешний для треугольника АВС. По свойству внешнего угла
∠BCD = ∠ABC + ∠BAC
∠BAC = ∠BCD - ∠ABC = 50° - 20° = 30°
∠DAB = 30°
_________________________________
Стоит запомнить, что угол между секущими, проведенными из одной точки (или между секущей и касательной, как в данном случае), равен полуразности дуг, заключенных между ними.
∠DAB = 1/2 (∪DB - ∪CB) = 1/2 (100° - 40°) = 1/2 · 60° = 30°
Ребро правильного тетраэдра равно 26 см. Вычисли площадь полной поверхности.
ответ: площадь поверхности равна: 3–√ см2.
Попроси больше объяснений
Следить
Отметить нарушение
Misatian17072004 2 недели назад
ответ
ответ дан
runrabbit

AB=AC=CB=SB=SC=SA=26м
У правильного тетраэдра все четыре грани — равностороннние треугольники. Площадь поверхности равна сумме площадей всех этих треугольников.
Sравн. Δ=a23√4, где a — сторона треугольника.
S=4⋅SABC=4⋅AB23√4=AB23√=2723√=7293√м2
Площадь поверхности тетраэдра равна 729 3√ м2
1) нарисуем трапецию АВСД. АД-большее основание, ВС- меньшее основание. Т.К угол В=120, то угол С=120 тоже. Проведем высоты ВН и СМ. В треуг., АВН: угол А=60(сумма всех углов трапеции= 360град;В+С=240;360-240=120; А=Д=60; ).угол Н=90, значит АВН=30. сторона, лежащая против угла в 30 гр., равна половине гипотенузы, значт АН=3см. Аналогично в треуг.,МСД. По теореме пифагора находим, что ВН=СН= корень из 27. ВС=НМ=4см. площадь АВСД= 1/2(4+10)*корень из27=7корень из 27.