Решить 2 по ! 1. радиус шара равен 6дм, через конец радиуса лежащего на сфере проведена плоскость под углом 30 градусов к радиусу. найдите sсечения плоскостью и sсферы. 2.через конец радиуса лежащего на сфере проведена плоскость под углом 60 градусов к радиусу. расстояние от центра сферы до этой плоскости 8см. найдите sсечения шара плоскостью и sсферы
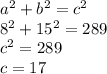
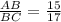 - то и есть коэффициент подобия этих треуг.
- то и есть коэффициент подобия этих треуг.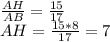
![\sqrt[n]{x}](/tpl/images/0258/0436/b773b.png)
1. R = 6 дм - радиус шара,
r - радиус сечения.
Отрезок ОС, соединяющий центр шара с центром сечения, перпендикулярен плоскости сечения.
ΔОСВ: ∠ОСВ = 90°, cos30° = r / R
r = R · cos30° = 6 · √3/2 = 3√3 дм
Sсеч. = πr² = 27π дм²
Sсферы = 4πR² = 4π · 36 = 144π дм²
2. ΔОСВ: ∠ОСВ = 90°, sin60° = OC/R
R = OC / sin60° = 8 / (√3/2) = 16/√3 см
r = R · cos60° = 16/√3 · 1/2 = 8/√3 см
Sсеч. = πr² = π · 64/3 = 64π/3 см²
Sсферы = 4πR² = 4π · 256/3 = 1024π/3 см²