Основанием пирамиды является прямоугольный треугольник с катетами 6 и 8 см. Боковые рёбра наклонены к плоскости основания под углом 45 градусов. Найти высоту пирамиды.
Если боковые рёбра наклонены к плоскости основания под одинаковым углом 45 градусов, то вершина пирамиды проецируется на основание в центр описанной окружности.
Для прямоугольного треугольника центр описанной окружности находится в середине гипотенузы.
Боковое ребро из прямого угла проецируется на медиану основания, которая равна √((6/2)² + (8/2)²) = √(9 + 16) = √25 = 5.
При угле ребра 45 градусов медиана равна высоте пирамиды.
ответ: высота пирамиды равна 5.
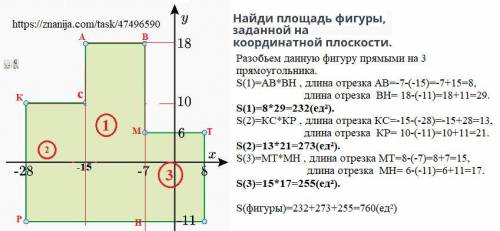
Найди площадь фигуры, заданной на координатной плоскости.
Объяснение:
Разобьем данную фигуру прямыми на 3 прямоугольника.
S(1)=АВ*ВН , длина отрезка АВ=-7-(-15)=-7+15=8,
длина отрезка ВН= 18-(-11)=18+11=29.
S(1)=8*29=232(ед²).
S(2)=КС*КР , длина отрезка КС=-15-(-28)=-15+28=13,
длина отрезка КР= 10-(-11)=10+11=21.
S(2)=13*21=273(ед²).
S(3)=МТ*МН , длина отрезка МТ=8-(-7)=8+7=15,
длина отрезка МН= 6-(-11)=6+11=17.
S(3)=15*17=255(ед²).
S(фигуры)=232+273+255=760(ед²)
Треугольник в основании имеет стороны (6, 25, 29). Его можно представить, как разность двух Пифагоровых треугольников - со сторонами (20, 21, 29) и (15, 20, 25).
Делается это так - на катете 21 треугольника (20, 21, 29) от вершины прямого угла откладывается 15 и соединяется с вершиной противоположного острого угла.
Этот "трюк" нужен для того, чтобы устно вычислить высоту (к стороне 6) и площадь треугольника (6, 25, 29). Высота равна 20, а площадь 60.
(Конечно, все это можно сделать "стандартными методами", то есть сообразить, что между сторонами 6 и 25 - тупой угол, продлить сторону 6 за вершину тупого угла, и опустить перпендикуляр из противоположной вершины. Затем записать теорему Пифагора для получившихся треугольников и решить её - как раз и получим ответ 20.
А можно - если совсем жалко мозги тратить - сосчитать площадь по формуле Герона. Получим 60 - можете проверить :)
Все эти методы - правильные, но у моего "неправильного" есть одно преимущество - ответ в одну секунду сам собой получается без всяких вычислений. Вернусь к задаче.)
Пусть высота призмы (боковое ребро) равно х. Тогда по условию
х*(6 + 25 + 29) + 2*60 = 1560; х = 24;
Объем 60*24 = 1440;
Объяснение: