1.
Площадь квадрата равна
S=a²
А значит просто подставляем сюда значение
S=9.1²дм=82,81дм²
2.
Сначала найдём площадь прямоугольника.Она ищется так
S=ab=18см×50см=900см²
Значит площадь квадрата тоже равна 900
Отсюда можно найти сторону квадрат
a=корню из площади S=корень из 900=30см
3.Давай посмотрим
Была сторона а=2,значит S=4
Увеличим а в 2 раза,а стало равно 4,а площадь 16
Для нагядного примера возьмём еще значения.
Например а=3,значит S=9
Увеличаем а в 2 раза,следовательно а=6,а S=36
Как видим везде площади увеличилсь в 4 раза
Значит ответ :в 4 раза
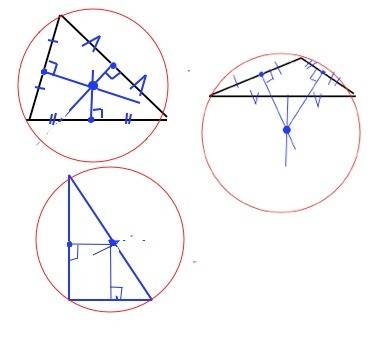
Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров.
Для остроугольного треугольника этот центр будет в треугольнике.
Построение.
Построить нужный треугольник не составляет труда.
1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. .
Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности.
Расстояние от него до вершин треугольника равны радиусу описанной окружности.
2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника.
3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны.
Как это выглядит, дано в приложении.
Треугольники, образованные биссектрисой am amb и amc равны, т.к. в равностороннем треугольнике биссектрисы, медтаны и высоты равны. Значит, равны и отрезки mb и mc.
Но эти отрезки не что иное, как проекции любой точки отрезка am на сторону bc.Значит любая точка отрезка am равноудалена от b и с.
Что и требовалось доказать.