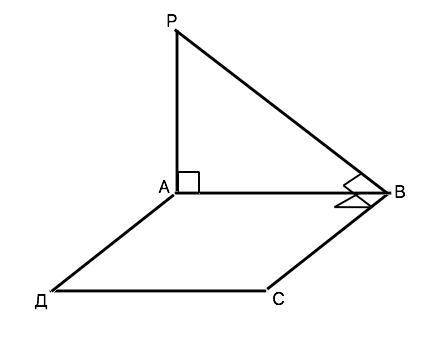
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
Свойство биссектрисы треугольника:
Биссектриса треугольника делит третью сторону на отрезки, пропорциональные двум другим сторонам.
Проведём биссектрисы углов В и С. Для этого высчитываем координаты точек К и М пересечения биссектрис со сторонами, используя их свойство.
Далее по координатам вершин В и С и найденных точек К и М определяем уравнения биссектрис.
Решая систему полученных уравнений находим координаты центра вписанной окружности.
Детальные расчёты приведены в приложении.
Но для данной задачи есть более простое решение.
Находим длины сторон треугольника.
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √9 = 3,r =(a+b-c)2 = (3+4-5)/2 = 1.
R = abc/(4S) = (3*4*5)/(4*((1/2)*3*4)) = 60/24 = 2,5.
2) координаты центра описанной окружности находятся на пересечении срединных перпендикуляров к сторонам треугольника.
12+6=18-abe
180:18=10-dvd
36+10=46-отношение s1:s2