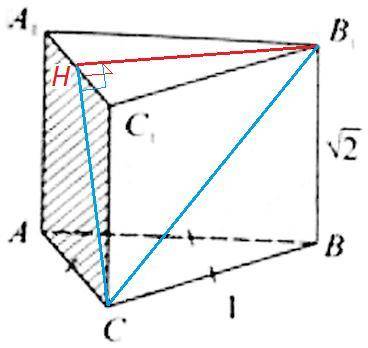
Угол между прямой и плоскостью - угол между наклонной и её проекцией на плоскость.
Чтобы найти проекцию наклонной B1C на плоскость (AA1C) спроецируем точку B1, то есть проведем перпендикуляр B1H к плоскости (AA1C).
Прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым в плоскости.
Любая прямая в плоскости (A1B1C1) перпендикулярна СС1 (боковые ребра прямой призмы перпендикулярны основаниям). Поэтому достаточно опустить перпендикуляр B1H на A1С1.
B1H⊥A1С1, B1H⊥CC1 => B1H⊥(AA1C)
HC - проекция наклонной B1C на плоскость (AA1C)
B1CH - искомый угол
△B1CH - прямоугольный (B1H⊥HC)
7) B1H =√3/2 (высота в равностороннем △A1B1C1)
B1C =√3 (△B1CB, теорема Пифагора)
sin(B1CH) =B1H/B1C =1/2
B1CH=30
8) HC1 =4 (B1H высота и медиана)
HC =5 (△HCC1 египетский)
cos(B1CH) =HC/B1C =5/10 =1/2
B1CH=60
a - сторона квадрата, вписанного в малый сегмент, b - в большой.
(a/2)^2 + (a + h)^2 = R^2; (b/2)^2 + (b - h)^2 = R^2;
5*a^2/4 + 2*a*h + h^2 = R^2; 5*b^2/4 - 2*b*h + h^2 = R^2;
a^2 + (8/5)h*a - (R^2 - h^2) = 0; b^2 - (8/5)h*b - (R^2 - h^2) = 0
a = -(4/5)*h + корень(((4/5)*h)^2 + (R^2 - h^2)); (отрицательный отброшен)
b = (4/5)*h + корень(((4/5)*h)^2 + (R^2 - h^2)); (отрицательный отброшен)
b - a = (8/5)*h;
Возможно, это можно как то увидеть с чисто геометрического построения, но я не нашел ...