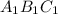Пирамида правильная, значит ее вершина проецируется в центр основания - точку О - центр описанной и вписанной окружностей.
SO=√13 (высота пирамиды - дана).
АВ=ВС=АС =6 (стороны основания - правильного треугольника - дано).
АН=(√3/2)*АВ (формула высоты правильного треугольника).
АН - высота, биссектриса и медиана =>
ОН=(1/3)*АН (свойство медианы).
Тогда
АН=(√3/2)*6=3√3.
ОН=(1/3)*3√3=√3.
SH=√(SO²-OH²)=√(13-3)=√10.
Sб=(1/2)*Р*SH =(1/2)*18*√10 (произведение полупериметра основания на высоту боковой грани (апофему).
Sб=9√10.
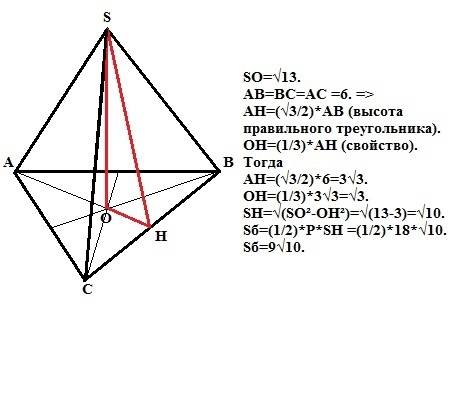
Дано: пирамида SABC. Основание АBС- прямоугольный треугольник с =90 градусов , АB = 15 см, AC = 9 см. Сечение пирамиды плоскостью, проходящей через середину O_{1} высоты SO пирамиды паралельно основанию, представляет собой прямоугольный треугольник