Вправильной четырехугольной пирамиде сторона основания равна 8см, а боковое ребро наклонено к плоскости основания под углом 45 градусов. найти площадь боковой поверхности пирамиды.
Поскольку четырехугольная пирамида ПРАВИЛЬНАЯ, то в основании лежит квадрат. Диагональ квадрата ABCD равен см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть см.
Из прямоугольного треугольника SOD: из определения косинуса найдем боковое ребро пирамиды:
см.
Высота SK равнобедренного треугольника SCD делит основание CD пополам, то есть: см
Тогда из прямоугольного треугольника SKC:
см. Тогда площадь грани SCD равна см²
Площадь боковой поверхности - это сумма всех площади граней. То есть, зная что у правильной пирамиды все грани равны, то площадь бок. пов.
Обозначим стороны треугольника a,b и c, где является гипотенузой. с=9+12. Не стоить забывать что треугольник прямоугольный, и когда опускается высота с прямоугольной вершины, то она делит наш треугольный на два подобных треугольника (угол 90/2, общая сторона - длина высоты, и углы под 90 градусов на гипотенузе). Так, приступим к теореме Пифагора для наших подобных треугольников: 9^2+x^2=a^2 16^2+x^2=b^2 а^2+b^2=c^2 9^2+x^2+16^2+x^2=(9+16)^2 2x^2+81+256=625 2x^2=288 x=12 (высота) 9^2+x^2=a^2 a^2=9^2+12^2 a^2=225 a=15 16^2+x^2=b^2 b^2=16^2+12^2 b^2=400 b=20 ответ: стороны треугольника а=15 см, b=20 см, с=25 см.
Для решения нужно вспомнить. что: Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому h²=9·16=144 h=12 Из треугольников. на которые высота поделила искходный треугольник, по теореме Пиагора найдем катеты: 1)9²+12²=225 √225=15 2)16²+12²=400 √400=20 Катеты равны 15см и 20 см, гипотенуза 9+16=25 см
Можно применить для решения другую теорему. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. Найдем гипотенузу: 9+16=25 см Пусть меньший катет будет х. Тогда его проекция - 9см: х²= 9·25=225 х=15 см Больший катет пусть будет у: у²=25·16=400 у=20 см
Поскольку четырехугольная пирамида ПРАВИЛЬНАЯ, то в основании лежит квадрат. Диагональ квадрата ABCD равен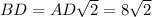 см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть
см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть 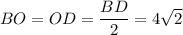 см.
см.
Из прямоугольного треугольника SOD: из определения косинуса найдем боковое ребро пирамиды:
Высота SK равнобедренного треугольника SCD делит основание CD пополам, то есть: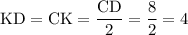 см
см
Тогда из прямоугольного треугольника SKC:
Площадь боковой поверхности - это сумма всех площади граней. То есть, зная что у правильной пирамиды все грани равны, то площадь бок. пов.
ответ: 64√3 см².