Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и притом только один.
Доказательство: предположим, что на плоскости, которой принадлежат и прямая, и точка, таких перпендикуляров существует два. Поскольку точка вне прямой принадлежит обоим перпендикулярам, получаем треугольник с вершиной в этой точке и основанием, расположенном на прямой. Так как оба перпендикуляра составляют с прямой углы по 90° (углы при основании треугольника) плюс угол при вершине, то сумма внутренних углов такого треугольника получается больше 180°, - а это на плоскости осуществить невозможно. Следовательно, наше предположение о том, что через одну точку к данной прямой на плоскости можно провести больше одного перпендикуляра, - не верно и такой перпендикуляр существует только один. Теорема доказана.
PS построения не сложные. - прямая, 2 точки на ней, одна точка вне прямой и два отрезка, соединяющие эту точку с точками на прямой..))) Но, если очень надо, - то файлик внизу с рисунком..)) И еще. Упоминание о том, что все это происходит на плоскости, - желательно. Дело в том, что всем нам с детства знакомы меридианы на географической сетке Земного шара. Так вот каждый меридиан перпендикулярен экватору, и все меридианы сходятся аж в двух точках : в Северном и Южном полюсах
Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию равнобедренного треугольника, совпадают между собой. Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны." Решение: Итак, треугольники АМD и DNC - равны между собой, так как AD=DC (BD- медиана), NC=МA (так как МВ=BN - дано, а АВ=ВС - треугольник АВС равнобедренный) и улы ВАС и ВСА между равными сторонами равны. Из равенства тр-ков вытекает равенство сторон МD и ND. Что и требовалось доказать
a = 5 см,
b = 4 см,
c = 7 см.
Найти R.
Запишем теорему синусов:
числитель и знаменатель дроби слева последнего равенства домножим на (b·c).
С учётом того, что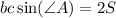 , где S - площадь данного в условии треугольника, имеем
, где S - площадь данного в условии треугольника, имеем
Площадь треугольника можно найти по формуле Герона:
Найдем, сначала, площадь треугольника.
p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.
S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²
Теперь найдем радиус описанной окружности.
R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.
Теперь найдём длину окружности, описанной около данного треугольника.
L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.