Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
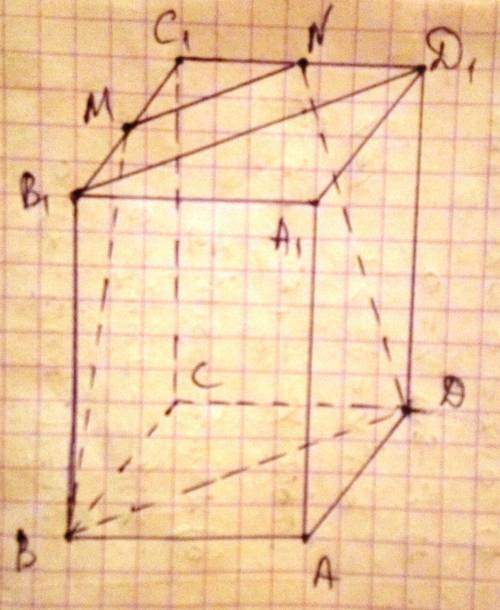
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
В любом параллелограмме стороны попарно равны и параллельны: АВ=СД, ВС=АС
Зная, что АС||ВД, можем утверждать, что:
Угол А+угол Б=180 градусов (смежные углы при АС||ВД и секущей АВ)
Пусть угол В=х, тогда угол А=х+20 (из условия).
Составим уравнение.
х+х+20=180
2х=160
х=80
Итак, угол В=80 градусов, а мы знаем, что в каждом параллелограмме противоположные углы равны, отсюда: угол В=угол Д=80 градусов
Найдём угол А: 180-угол В=180-80=100 градусов. Аналогично: угол А=угол С=100 градусов
ответ: угол А=100 градусов
угол В=80 градусов
угол С=100 градусов
угол Д=80 градусов
т.к. треугольник АВС - р\б, то углы при основании равны.
угол АКС = 60
угол А = углу С, угол ВСК = углу КСА = 1\2 угла С, следовательно угол КСА = 1\2 угла А
дальше решаем уравнением :
пусть угол КСА = х,
тогла угол А = 2х
2х+х = 120
3х = 120
х= 40 к
угол КСА = 40 , тогда угол А = 40
, тогда угол А = 40 * 2 = 80
* 2 = 80
угол А = 80
угол А = углу С, следовательно угол С = 80
сумма углов треугольника равна 180 , следовательно 180
, следовательно 180 - 80
- 80 * 2 = 20к
* 2 = 20к
угол А = углу С = 80 , угол В = 20
, угол В = 20