Довжина другої похилої 24.7 cм
Объяснение:
Відстань від точки до прямої дорівнює
h=24*sin45°=12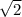
cм
Довжина другої похилої дорівнює
в=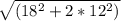
=24.7 cм
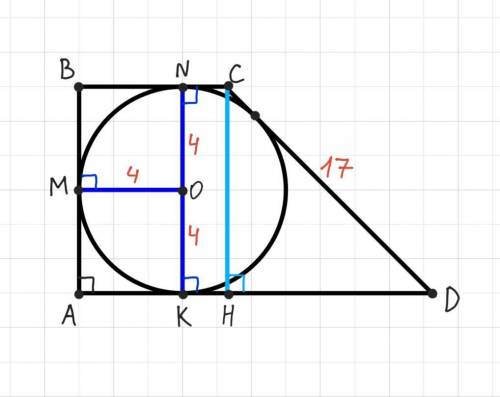
Дано: ABCD - прямоугольная трапеция (BC||AD, AB⊥AD), окружность, впис. в ABCD, R= 4, CD = 17 см.
Найти: BC, AD.
Решение.
Проведём высоту СН.
Диаметр NK, проведённый через точки соприкосновения окружности, равен высоте СН. Также, высота и боковая сторона прямоугольной трапеции, прилежащая к прямому углу, равны. СН=NK=AB.
NK=CH=AB=d= 2R= 2•4= 8 (см).
В прямоугольном ΔCHD (∠CHD=90°) по т. Пифагора:
HD²= CD² - CH²;
HD²= 17² - 8²;
HD²= 289 - 64;
HD²= 225;
HD= 15 (-15 не подходит).
AD= AH+HD, AH=BC (поскольку AB и CH высоты), значит, AD= BC+HD => AD= BC+15.
Свойство трапеции, в которую вписана окружность:
если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
Отсюда, BC+AD=AB+CD,
BC+ (BC+15)= 8+17;
2BC+ 15= 25;
2BC= 10;
BC= 5 (см).
Значит, AD= 5+15= 20 см.
ОТВЕТ: 5 см, 20 см.
Дано:
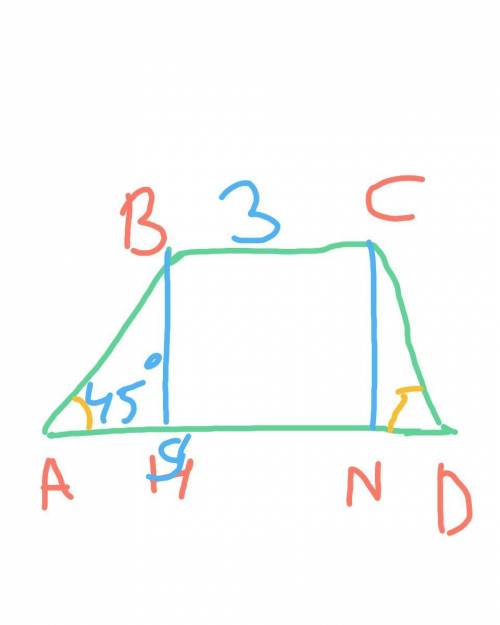
АBCD - равнобедренная трапеция;
АВ = СD (боковые стороны);
BC (основание) = 3;
AD (основание) = 9;
Угол DAB = углу ADC = 45°;
BH и СN - высоты АВСD.
Найти: S (ABCD).
1) Рассмотрим прямоугольник HBCN (т. к. BH и CN - высоты АВCD):
▪ВС=HN=3 см (по свойству противоположных сторон параллелограмма).
2) AH = DN = (AD - HN) : 2 = (9 см - 3 см) : 2 = 6 см : 2 = 3 см.
3) Угол АВС = углу BCD (т. к. ABCD - равнобедренная трапеция) = (360° (сумма всех углов четырёхугольника) - угол DAB - угол ADC) : 2 = (360° - 45° - 45°) : 2 = 270° : 2 = 135°.
4) Рассмотрим прямоугольный треугольник АВН (т. к. ВН - высота ABCD):
▪Угол АВН = угол АВС - угол СBH = 135° - 90° (т. к. ВН - высота ABCD) = 45° => угол DAB = углу АВН = 45° => АВН - равнобедренный треугольник с прямым углом Н => АВ = BH.
5) ...
2√153 см ≈ 24,74 см
Объяснение:
1) 24 - це довжина гіпотенузи; а тому кут, який вона утворює з прямою дорівнює 45°, то обидва катета (один з них - довжина проекції, а інший-висота, відстань від точки до прямої) рівні. Приймемо довжину катета за х.
Тоді, згідно з теоремою Піфагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Довжину другої похилої L знаходимо також за теоремою Піфагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
Відповідь: 2√153 см ≈ 24,74 см
1) 24 - это длина гипотенузы, а т.к. угол, который она образует с прямой равен 45°, то оба катета (один из них - длина проекции, а другой - высота, расстояние от точки до прямой) равны. Примем длину катета за х.
Тогда, согласно теореме Пифагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Длину второй наклонной L находим также по теореме Пифагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см