Дважды два четыре дважды два четыре
Это всем известно в целом мире
Дважды два четыре дважды два четыре
Это всем известно в целом мире
Дважды два четыре дважды два четыре
А не три а не пять это надо знать
Дважды два четыре дважды два четыре
А не шесть а не семь это ясно всем
Трижды три навеки девять
Ничего тут не поделать
И не трудно сосчитать
Сколько будет пятью пять
Пятью пять двадцать пять
Пятью пять двадцать пять
Совершенно верно
Дважды два четыре дважды два четыре
Это всем известно в целом мире
Дважды два четыре дважды два четыре
Это всем известно в целом мире
Дважды два четыре дважды два четыре
А не три а не пять это надо знать
Дважды два четыре дважды два четыре
А не шесть а не семь это ясно всем
У кого друзья ни спросим
Шестью восемь сорок восемь
Шестью шесть учесть
Неизменно тридцать шесть
Шестью шесть тридцать шесть
Шестью шесть тридцать шесть
Совершенно верно
Дважды два четыре дважды два четыре
Это всем известно в целом мире
Дважды два четыре дважды два четыре
Это всем известно в целом мире
Дважды два четыре дважды два четыре
А не три а не пять это надо знать
Дважды два четыре дважды два четыре
А не шесть а не семь это ясно всем
Дважды два четыре дважды два четыре
А не три а не пять это надо знать
Дважды два четыре дважды два четыре
А не шесть а не семь это ясно всем
Объяснение:
Кароч дважды два - ЧЕТЫРЕ
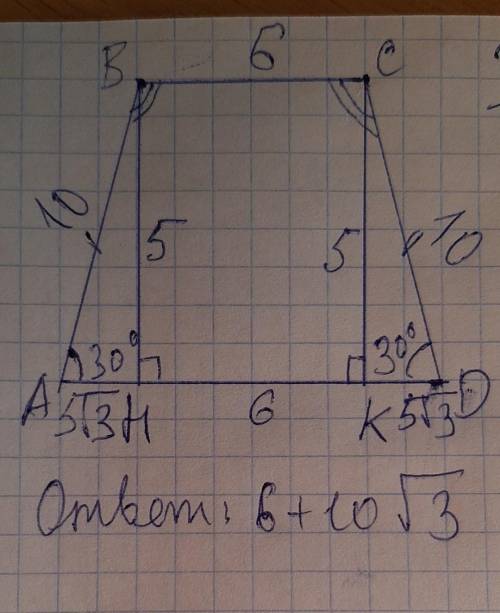
Решение: Проведём высоту СК.
Значит, BHKC прямоугольник, тогда ВС=HK=6 , BH=CK=5.
В треугольнике АВН угол АНВ= 90°, значит треугольник АВН - прямоугольный, т.к. угол А=30° и катет ВН=5, то гипотенуза АВ= 10 ( т.к. в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы).
Т.к. АВСD - равнобедеренная трапеция, то угол А = углу D = 30°.
Значит треугольник АВН= треугольнику СКD (по гипотенузе и острому углу)
Треугольнике АВН - прямоуольный:
По теореме Пифагора:
АН² + ВН²= АВ²
АН² = АВ² - ВН²
АН² = 100 - 25 = 75
АН = корень в квадрате из 75 = 5 корней из трёх
АН = КD = 5 корней из трёх
АD = 6 + 5 корней из трёз + 5 корней из трёх = 6 + 10 корней из трёх.
ответ: 6 + 10 корней из трёх.
41° 57° 82°
Объяснение:
Будем использовать следующие значения для сторон треугольника АВС: АВ=с, ВС=а, СА=b и его углов:
<А=а, <В=b, <C=y (a, b, y : Альфа, Бэта, Гама.)
Дано:
а=4, b=5, c=6.
Найти: a, b, y -?
Пусть b - наибольшая сторона, b<a+c.
По теореме косинусов находим наибольший угол b,
[Не обязательно писать, для ориентира: Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.]
{b}^{2} = {a}^{2} + {c}^{2} - 2ac \times cos \betab
2
=a
2
+c
2
−2ac×cosβ
\begin{gathered} \cos\beta = \frac{a {}^{2} + c {}^{2} - b {}^{2} }{2ac} = \frac{16 + 36 - 25}{48} = 0,5625 = \\ = \frac{9}{16} \end{gathered}
cosβ=
2ac
a
2
+c
2
−b
2
=
48
16+36−25
=0,5625=
=
16
9
При основного тригонометрического тождества найдём Sin B
\begin{gathered}sin {}^{2} \beta + cos {}^{2} \beta = 1 \\ sin {}^{2} \beta = 1 - cos {}^{2} \beta \\ sin \beta = \sqrt{1 - \frac{81}{256} } = \\ = \sqrt{ \frac{175}{256} } = \frac{5 \sqrt{7} }{16} \end{gathered}
sin
2
β+cos
2
β=1
sin
2
β=1−cos
2
β
sinβ=
1−
256
81
=
=
256
175
=
16
5
7
С теоремы синусов найдём углы треугольника:
\frac{a}{ \sin( \alpha ) } = \frac{b}{ \sin( \beta ) } = \frac{c}{ \sin( \gamma ) }
sin(α)
a
=
sin(β)
b
=
sin(γ)
c
Отсюда,
\sin( \alpha ) = \frac{a \sin( \beta ) }{b} = \frac{5 \sqrt{7} }{4} \times \frac{1}{5} = \frac{ \sqrt{7} }{4}sin(α)=
b
asin(β)
=
4
5
7
×
5
1
=
4
7
\sin( \gamma ) = \frac{c\sin( \beta ) }{b} = \frac{5 \sqrt{7} }{ 16} \times \frac{6}{5} = \frac{3 \sqrt{7} }{8}sin(γ)=
b
csin(β)
=
16
5
7
×
5
6
=
8
3
7
С таблиц находим градусную меру углов:
а≈41°
b≈57°
Тогда,
у≈82°
ответ: 41° 57° 82°