Пусть дана пирамида РАВС. РВ - её высота, АС - гипотенуза основания.
Гипотенуза основания равна 12√2 см.
Высота из точки В на АС в прямоугольном равнобедренном треугольнике является медианой. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы. То есть она равна 6√2 см.
Находим высоту боковой грани АРС:
РК = √(9² + (6√2)²) = √(81 + 72) = √153 = (3√17) см.
Находим площадь боковой поверхности.
Sбок = 2*(1/2)*9*12 + (1/2)*12√2*3√17 = (108 + 18√34) см².
Площадь основания So = (1/2)*12² = 72 см².
Площадь полной поверхности равна:
S = So + Sбок = 72 + 108 + 18√34 = (180 + 18√34) см².
Симметрия относительно точки предполагает, что по обе стороны от точки на одинаковых расстояниях находится что-либо, например другие точки или геометрическое место точек (прямые линии, кривые линии, геометрические фигуры).
Если соединить прямой симметричные точки (точки геометрической фигуры) через точку симметрии, то симметричные точки будут лежать на концах прямой, а точка симметрии будет ее серединой. Если закрепить точку симметрии и вращать прямую, то симметричные точки опишут кривые, каждая точка которых тоже будет симметрична точке другой кривой линии.
Симметрия относительно прямой (оси симметрии) предполагает, что по перпендикуляру, проведенному через каждую точку оси симметрии, на одинаковом расстоянии от нее расположены две симметричные точки. Относительно оси симметрии (прямой) могут располагаться те же геометрические фигуры, что и относительно точки симметрии.
Примером может служить лист тетради, который согнут пополам, если по линии сгиба провести прямую линию (ось симметрии). Каждая точка одной половины листа будет иметь симметричную точку на второй половине листа, если они расположены на одинаковом расстоянии от линии сгиба на перпендикуляре к оси.
центральная и осевая симметрия
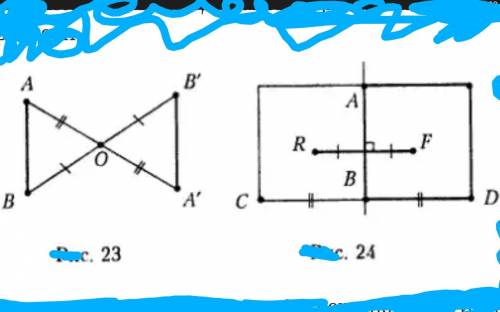
Линия осевой симметрии, как на рисунке 24, вертикальна, и горизонтальные края листа перпендикулярны ей. Т. е. ось симметрии служит перпендикуляром к серединам горизонтальных ограничивающих лист прямых. Симметричные точки (R и F, C и D) расположены на одинаковом расстоянии от осевой прямой — перпендикуляра к прямым, соединяющим эти точки. Следовательно, все точки перпендикуляра (оси симметрии), проведенного через середину отрезка, равноудалены от его концов; или любая точка перпендикуляра (оси симметрии) к середине отрезка равноудалена от концов этого отрезка.
на скрине всё написано)
Объяснение: