Пусть данная точка будет А, плоскости, между которыми она расположена – α и β.
Расстояние от точки до плоскости - длина отрезка, проведенного перпендикулярно к ней.
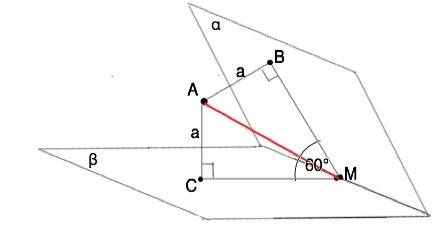
АВ ⊥ альфа, АС ⊥ бета. АВ=АС=а
Расстояние от точки до линии пересечения плоскостей - длина отрезка, проведенного перпендикулярно этой линии, т.е. ребру двугранного угла. АВ и АС лежат в плоскости, перпендикулярной двугранному углу, т.е. содержащей его линейный угол. АМ лежит в той же плоскости и потому перпендикулярна линии пересечения плоскостей.
ВМ и СМ - проекция наклонной АМ на данные плоскости, а т.к. расстояния от А до них равны, то ВМ=СМ.
Рассмотрим треугольники АВМ и АСМ. Оба прямоугольные с равными катетами и общей гипотенузой АМ. ⇒∆ АВМ=∆АСМ по трем сторонам.
∠АМВ=∠АМС=60°:2=30° ⇒
АМ=АВ:sin30°=а:1/2=2a Это ответ.
ответ: 20 см
Решение: смотри рисунок.
Пусть треугольник BAC равнобедренный, AB=AC=10 см.
Возьмем произвольную точку K на основании BC и проведем KM||AC иKN||AB
KM=AN, KN=AM -противоположные стороны параллелограмма.
Докажем, что KM=BM. Угол 2=углу 4 как соответственные углы при AC||KM и секущей KC. Но угол 4=углу 1 (углы при основании равнобедренного треугольника). Отсюда угол 2=углу 1. Значит треугольник BMK равнобедренный и KM=BM как его боковые стороны.
Аналогично докажем, что KN=NC. Угол 3=углу 1 как соответственные углы при AB||KN и секущей KB. Но угол 1=углу 4 (углы при основании равнобедренного треугольника). Отсюда угол3 =углу 4. Значит треугольник KNC равнобедренный и KN=NC как его боковые стороны.
Периметр параллелограмма =KM+MA+AN+NK=BM+MA+AN+NC=BA+AC=10+10=20 (см)