Воспользуемся формулой вычисления медианы:
m(a)=0,5*корень из выражения 2b^2+2c^2-a^2, где m(a)-медиана, проведенная к основанию a. Так как треугольник равнобедренный, то b=c, значит, можем написать вместо 2b^2+2c^2= 4b^2.
подставим в формулу значения
12=0,5*корень из выражения 4b^2-18^2
24=корень из выражения 4b^2-324
возводим в квадрат обе части выражения, чтобы извавиться от корня, получаем:
576=4b^2-324
900=4b^2
b^2=225
b=15. Значит ребра треугольника равны 15.
Pтреугольника=a+b+c=15+15+18=48.
ответ: 48.
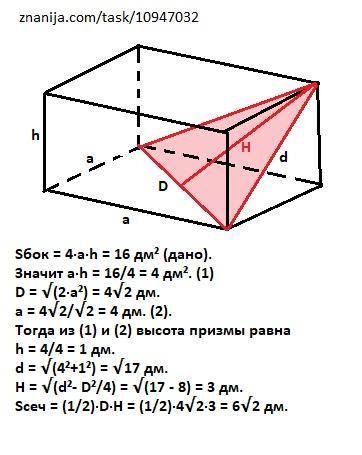
Sсеч = 6√2 дм.
Объяснение:
У правильной четырехугольной призмы основания (нижнее и верхнее) - квадраты, боковые грани (их четыре) - равные прямоугольники со сторонами, равными стороне основания и высоте призмы.
Площадь боковой поверхности призмы - Sбок = 4·a·h = 16 дм² (дано). Значит a·h = 16/4 = 4 дм². (1)
Диагональ основания (квадрата) равна по Пифагору:
D = √(2·а²) = 4√2 дм.
Значит сторона основания а = 4√2/√2 = 4 дм. (2)
Тогда из (1) и (2) высота призмы равна h = 4/4 = 1 дм.
Сечение призмы, проходящее через диагонали двух смежных боковых граней, имеющих общую вершину - это равнобедренный треугольник с основанием - диагональю основания призмы и боковыми сторонами - диагоналями боковых граней.
Найдем диагональ боковой грани по Пифагору: d = √(a²+h²).
d = √(4²+1²) = √17 дм.
Найдем высоту равнобедренного треугольника по Пифагору:
Н = √(d²- D²/4) = √(17 - 8) = 3 дм.
Тогда площадь сечения равна:
Sсеч = (1/2)·D·H = (1/2)·4√2·3 = 6√2 дм.
Поскольку медиана равнобедреного триугольника есть ещо й висотой, то она утв. два прямоугольние трикутники. За означенням медіани, вона ділить основу на два рівні відрізки по 18/2=9см. Розглянемо "внутрішні" трикутники, утворені медіаною, половиною основи та стороною. За теоремою Піфагора: сторона^2=медіана^2+ 1/2основи ^2
х ^2 =12 ^2 +9 ^2
х ^2 = 144+81
х ^2 =225
х=15
Периметр - сума всіх сторін= 15+15+18=48