В условии, очевидно, ошибка: треугольник АВС с такими сторонами не существует, так как любая сторона треугольника меньше суммы двух других сторон, а 6 > 4 + 1.
Эта задача на тему "Подобие треугольников" . Решим ее для ВС = 7 см.
АВ : MK = 4 : 8 = 1/2
AC : MN = 6 : 12 = 1/2
BC : KN = 7 : 14 = 1/2
Значит ΔАВС подобен ΔMKN по трем пропорциональным сторонам.
Сумма углов треугольника равна 180°, значит
∠С = 180° - (∠А + ∠В) = 180° - (80° + 60°) = 180° - 140° = 40°
В подобных треугольниках напротив сходственных сторон лежат равные углы:
∠N = ∠С = 40°,
∠K = ∠В = 60°,
∠M = ∠А = 80°.
Объяснение:
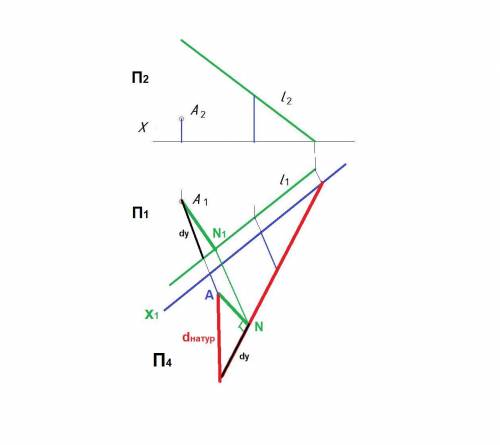
Надо перевести прямую в положение, параллельное плоскости проекции. Для этого используется метод замены плоскостей, который не предполагает перемещение фигур в пространстве.
Параллельно проекции l введена дополнительная фронтальная плоскость П4. В новой системе (П1, П4) точки находятся на том же удалении от оси X1, что и на фронтальной проекции.
Далее опускаем перпендикуляр из А1 на прямую l1, поскольку прямой угол проецируется на плоскость П4 в натуральную величину. По линии связи определяем положение точки N' и проводим проекцию A'N' отрезка AN.
На заключительном этапе определяем величину отрезка AN по его проекции на плоскости П4 и dy. Для этого строим прямоугольный треугольник, у которого катет равен разности dy удаления точек A и N от оси X1. Длина гипотенузы треугольника соответствует искомому расстоянию от A до l.
2.(302 281 - 12 649) ÷ 48 + 3 966
302281-12649=289 632
289632÷48=6034
6034+3966=10000
3.(21000-308-29)÷4+14147÷47
14147÷47=301
21000-308-29=20663
20663÷4=5165.75
5165.75+301=5 466,75
1.(90050-219.380+190)÷90
(90050-219.380+190)=90 020,62
90 020,62÷90=1 000,2291111111