20°
Объяснение:
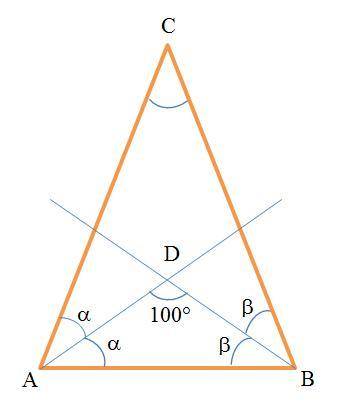
Дано (см. рисунок):
ΔАВС - равнобедренный
AD - биссектриса угла А
BD - биссектриса угла В
∠ADB = 100°
Найти: ∠С
Решение.
Так как треугольник ABC равнобедренный, то у него углы при основании равны ∠А=∠В. Биссектриса делит угол пополам, поэтому α=∠А/2 и β=∠В/2. Но ∠А=∠В и поэтому α=β. Значит, треугольник ADB также равнобедренный.
Найдём углы α и β. Сумма внутренних углов треугольника равна 180°: α + β + 100° = 180°. В силу этого α = β = (180-100)/2 = 40°.
Тогда ∠CАВ=∠СВА=2·α=2·40°=80°. Опять используем свойство:
Сумма внутренних углов треугольника равна 180°.
В силу этого ∠CАВ+∠СВА+∠С=180°. Отсюда
∠C=180°-(∠CАВ+∠СВА)=180°-(80°+80°)=180°-160°=20°.
ответ: 20°
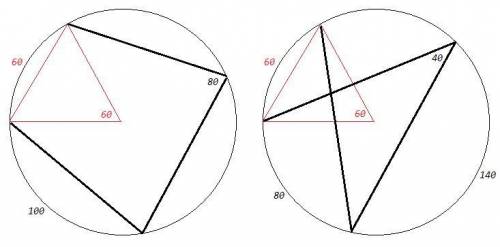
Хорда, равная радиусу, образует с радиусами равносторонний треугольник, следовательно стягивает дугу 60 (центральный угол равен дуге, на которую опирается).
1) Равные звенья стягивают равные дуги (360-60)/3 =100
Дуга между соседними звеньями 100+60=160
Вписанный угол, опирающийся на эту дугу 160/2=80
2) Ломаная может иметь одно самопересечение (очевидно, что соседние звенья не пересекаются, так как уже имеют общую точку). Тогда две дуги имеют общую часть 60 градусов.
Равные звенья стягивают равные дуги (360+60)/3 =140
Дуга между соседними звеньями 140-60=80
Вписанный угол, опирающийся на эту дугу 80/2=40
АВ=4, АМ=3, значит МВ=1, тоже самое и для ДК
Так как АВ параллельно ДС, то МВ параллельно ДК
раз две противоположные стороны параллельны и одинаковой длины, то это параллелограмм