Пусть ABCD некий прямоугольник, где противолежащие стороны и углы равны, тогда AB=CD и AC=BD, по условию нам известно что некая сторона теугольника равна 40 см, тогда AB=CD= 40 см. Мы знаем что при проведение диагоналей СB и DA прямоугольник делятся на два равных по 1-ому признаку равнобедренных прямоугольных прямоугольника. По теореме Пифагора мы сможем найти сторону AB:
A2 + B2= C2 (квадрат гипотенузы равен сумме квадратов катетов)
402+ B2= 412
1600+ B2=1681
B2=1681-1600
B2=81
B=√81
B=9
так как AB и CD равны как противолежащие стороны прямоугольник, то AB=CD=9 см.
Найдём площадь прямоугольника по формуле: S=ab; S= 40x9=360 см2
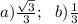
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
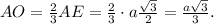
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
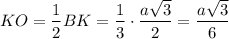
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
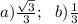
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
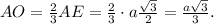
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
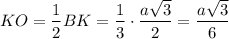
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.

вторая сторона = корень(диагональ в квадрате - сторона1 в квадрате) =корень(1681-1600)=9
площадь = сторона1 х сторона2 = 40 х 9 =360