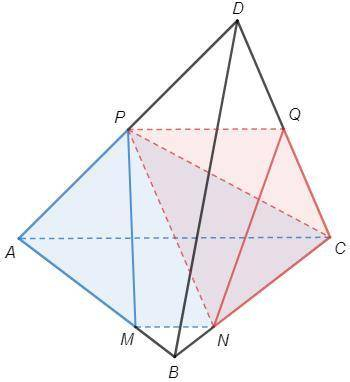
На ребрах AB и CB треугольной пирамиды DABC отмечены точки М и N, AM:MB=CN:NB=3:1. P и Q - середины ребер DA и DC. В каком отношении плоскость PQM делит пирамиду?
PQ||AC, MN||AC (по т о пропорциональных отрезках) => PQ||MN
Через две параллельные проходит плоскость PQMN
Рассмотрим пирамиду с основанием AMNC и вершиной P.
△MBN~△ABC, k=MB/AB=1/4
S(MBN)/S(ABC) =k^2 =1/16 => S(AMNC)/S(ABC) =15/16
Высоты из P и D на (ABC) относятся 1:2
V(PAMNC)/V(DABC) =15/16 *1/2 =15/32
Рассмотрим пирамиду с основанием QNC и вершиной P.
S(QNC)/S(DBC) =CQ*CN/CD*CB =CQ/CD *CN/CB =1/2 *3/4 =3/8
Высоты из P и A на (DBC) относятся 1:2
V(PQNC)/V(ADBC) =3/8 *1/2 =3/16
V(PAMNC)+V(PQNC) =(15/32 +3/16) V(DABC) =21/32 V(DABC)
Плоскость PQM делит пирамиду DABC в отношении 11:21.
Большая часть 21/32 от объема DABC.
Объяснение:
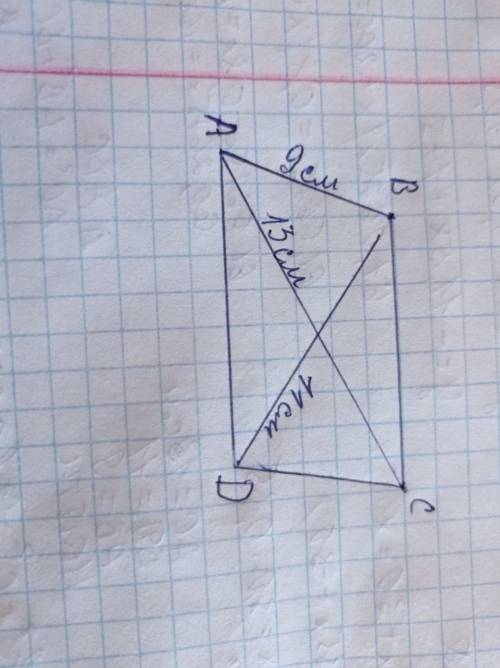
Дано:
АС = 13 см
ВD = 11 см
АВ = 9 см
Знайти: Р (АВСD) - ?
α - гострий кут між діагоналями
а² = b² + c² - 2bc *соs α
соs (180 - α) = - соs α
Розглянемо трикутник АВС по теоремі косінусів
АС² = АВ² + ВС² - 2 АВ * ВС * соs α
Розглянемо трикутник ABD
BD² = AB² + AD² - 2 AB * AD * соs α
∠A = ∠В = 180° BC = AD = x
Звідси маємо:
{13² = 9² + х² - 2* 9x* соs ∠В
{11² = 9² + х² - 2* 9x* соs ∠ А
{∠ А = 180° - ∠В => соs ∠ А = соs(180° - ∠В) = - соs ∠В
{169 = 81 + х² - 18x соs ∠В
{121² = 81 + х² + 18 x* соs ∠ B
Складемо рівняння (1) та (2)
290 = 162 + 2х²
128 = 2 х²
х² = 128 :2
х² = 64
х = 8 см
Периметр паралелограма дорівнює Р = 2 (9 + 8) = 34 (см)