
потенциальная энергия равна mgh
после отклонения шарика на 30градусов, а значит шарик стал выше над поверхностью, чем был до этого. чтобы найти новую высоту - h1.
h1 = изменение высоты+h
изменение высоты мы возмем из образовавшегося треугольника с углом 30 градусов и стороной(самой нитью) 30 градусов нить будет являться гипотенузой, а катет на против угла 30 равен половине гипотенузы(10см) но это нижний катет
теперь по т.Пифагора посчитаем второй катет(находящийся там, где в начальный момент была нить) L=  = 10
= 10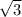
ну а теперь найдем изменение:
20-10*корень 3
получается что новая потенциальная энергия будет равна:
mg(h+20-10*корень3) из полученного выражения можем сделать вывод, что кинетическая энергия возросла
10. Где рес
11. Да
Объяснение: