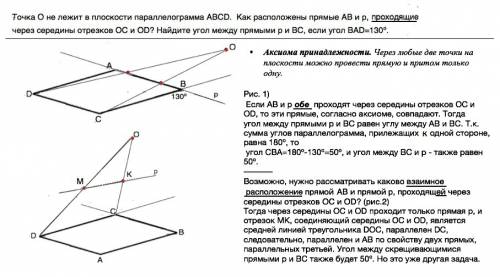
Точка О не лежит в плоскости параллелограмма ABCD. Как расположены прямые AB и p, проходящие через середины отрезков OC и OD? Найдите угол между прямыми p и BC, если угол BAD=130º
––––––––––––
Аксиома . Через любые две точки на плоскости можно провести прямую и притом только одну.. Если АВ и р обе проходят через середины отрезков ОС и ОD, то эти прямые, согласно аксиоме, совпадают. Тогда угол между прямыми р и ВС равен углу между АВ и ВС. Т.к. сумма углов параллелограмма, прилежащих одной стороне, равна 180º угол СВА=180º-130º=50º
–––––––
Возможно, нужно рассматривать каково взаимное расположение прямой AB и прямой p, проходящей через середины отрезков OC и OD, но расположенной в другой плоскости?
Тогда через середины ОС и ОD проходит только прямая р, и отрезок МК, соединяющий середины ОС и ОD, является средней линией треугольника DОC, параллелен DC, следовательно, параллелен и АВ по свойству двух прямых, параллельных третьей. Угол между скрещивающимися прямыми р и ВС также будет 50º. Но это уже другая задача.
Биссектриса делит угол пополам, т.е. ∠ABD = ∠DBC; ∠BAD=∠DAC.
1) \sf \angle \,BAD=\frac{1}{2}\angle\, A=\frac{1}{2}\cdot 50^\circ=25^\circ∠BAD=21∠A=21⋅50∘=25∘
\sf \angle\, ABD=\frac{1}{2}\angle \, B=\frac{1}{2}\cdot100^\circ=50^\circ∠ABD=21∠B=21⋅100∘=50∘
И рассмотрим треугольник ABD в нем сумма углов должна быть равна 180°,т.е. \sf \angle \,ADB=180^\circ-25^\circ-50^\circ=105^\circ∠ADB=180∘−25∘−50∘=105∘
2) Аналогично с примером 1)
\sf \angle \,BAD=\frac{1}{2}\angle\, A=\frac{1}{2}\cdot \alpha=\frac{\alpha}{2}∠BAD=21∠A=21⋅α=2α
\sf \angle\, ABD=\frac{1}{2}\angle \, B=\frac{1}{2}\cdot\beta=\frac{\beta}{2}∠ABD=21∠B=21⋅β=2β
\sf \angle \,ADB=180^\circ-\frac{\alpha}{2}-\frac{\beta}{2}=180^\circ-\frac{1}{2}(\alpha+\beta)∠ADB=180∘−2α−2β=180∘−21(α+β)
3) Сумма углов треугольника ABC равна 180°, т.е. ∠A+∠B+∠C=180°.
∠A + ∠B + 130° = 180°
∠A + ∠B = 180° - 130°
∠A + ∠B = 50°
∠ADB = 180° - 1/2(∠A + ∠B) = 180° - 1/2 * 50° = 180° - 25° = 155°
4) Аналогично с примером 3)
∠A + ∠B + ∠C = 180°
∠A + ∠B + \gammaγ = 180°
\sf \angle\, A+\angle \, B=180^\circ-\gamma∠A+∠B=180∘−γ
Тогда
\begin{gathered}\sf \angle\, ADB=180^\circ-\frac{1}{2}(\angle \, A+\angle \, B)=180^\circ-\frac{1}{2}(180^\circ-\gamma)=180^\circ-90^\circ+\frac{\gamma}{2}=\\ \\ =90^\circ+\frac{\gamma}{2}\end{gathered}∠ADB=180∘−21(∠A+∠B)=180∘−21(180∘−γ)=180∘−90∘+2γ==90∘+2γ