1.Дано: а || b, с - секущая, ∠1 - ∠2 = 102°. Найти: все образовавшиеся углы. 2.Дано: ∠1 = ∠2, ∠3 = 140°. - id1674540720230224 от katenkafialkaowy2yf 24.02.2023 02:50

Question

Геометрия: 1.Дано: а || b, с - секущая, ∠1 - ∠2 = 102°. Найти: все образовавшиеся углы. 2.Дано: ∠1 = ∠2, ∠3 = 140°. Найти: ∠4. 3. Отрезок АК - биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне С А и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если ∠CAE = 78°. 4*. Прямая MN является секущей для прямых АВ и CD (М ∈ АВ, N ∈ CD). Угол AMN равен 75°. При каком значении угла CNM прямые АВ и CD могут быть параллельными? ​

katenkafialkaowy2yf · Accepted Answer

Окружность, уравнение которой x^2+y^2 = 4 - это окружность с центром в начале координат радиусом 2., поскольку уравнение окружности таково: (x - a)^2 + (y - b)^2 = R^2 с центром в точке O(a;b) Радиуса R. Из условия имеем: (x - 0)^2 + (y - 0)^2 = 2^2. Далее, Из условия AB = BM. Рассмотрим это со следующего ракурса: AB = BM - радиусы некоторой окружности. На рисунке как бы мы не проводили хорду АВ, АВ будет равна ВМ и точка М будет лежать на той самой окружности. И хорда АМ большой окружности будет делится надвое радиусом в точке меньшей окружности (B, B1, B2 ... Bn). Получается, множество точек М - это некая окружность с центром B(2;0) радиусом 4. И уравнение такой окружности будет иметь вид: (x-2)^2 + y^2 = 16.

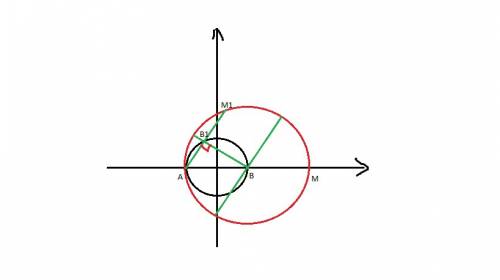
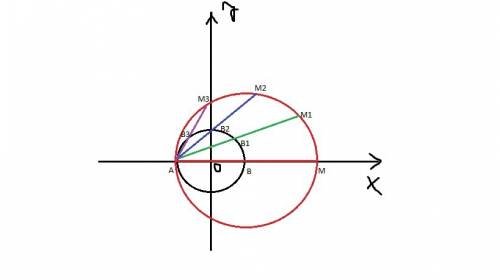
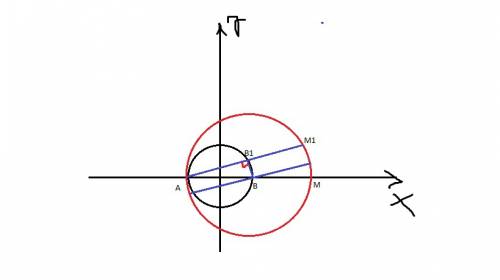
25 за подробное решение : дана окружность х² + у²=4 . из точки а(-2; 0) проведена хорда ав, которая

25 за подробное решение : дана окружность х² + у²=4 . из точки а(-2; 0) проведена хорда ав, которая

MOGZ ответил