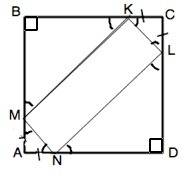
∆ KCL=∆ MAN по двум сторонам и углу между ними. ⇒ MN=KL.
Стороны квадрата равны. Если от равных отрезков отнять по равной части, оставшиеся отрезки будут равны. ⇒
МВ=ВК=LD=ND. -⇒ Прямоугольные ∆ МВК=∆ LDN.
Четырехугольник MNKL – параллелограмм.
Рассмотрим его углы на примере развернутого угла ВМА.
Так как стороны параллелограмма отсекают от углов квадрата равнобедренные прямоугольные треугольники, ∠ВМК=∠NMА=45°. Поэтому ∠КМN=180°-2•45°=90°
Противолежащие углы параллелограмма равны ( можно доказать для каждого угла, что он равен 90°). Тогда сумма двух противолежащих прямых углов равна 180°, и каждый из оставшихся также равен 90°.
Следовательно, четырехугольник КМNL- прямоугольник.
Проведем высоту из точки A в ΔABC и высоту из точки D в треугольнике CDB. Эти две высоты падают на одну точку, пусть на точку H. По определению, ∠AHD это и есть угол между плоскостями ABC и CDB.
В ΔAHD, AD = 1.
AH = DH = √(AB² - (0.5BC)²) = √(1² - 0.5²) = √(3/4) = √3 / 2
По теореме косинусов:
∠AHD = arccos(1/3)
ответ: arccos(1/3)