1. Верно ли следующее утверждение? А. На физических картах абсолютную высоту указывают не только для рельефа, но и для отдельных точек глубин водных объектов.
Б. Самое глубокое место на земном шаре - Пуэрториканский желоб.
послойной окраски- это:
А окраски географических объектов на картах.
Б отображения рельефа на картах.
В отражения материков на картах.
Г отражения океанов на картах.
3. Изобаты - это:
А. линии, соединяющие одинаковые значения абсолютных высот.
Б. линии, соединяющие одинаковые значения высот местности.
В. линии, соединяющие одинаковые значения глубин.
Г. линии, соединяющие одинаковые значения относительных высот.
4. Глубину объектов отображают цветовым фоном от
А. светло- желтого до темно- коричневого.
Б. светло- зеленого до темно- зеленого.
В. светло- желтого до темно- оранжевого.
Г. светло- голубого до темно- синего.
5. Определите, какие из следующих утверждений являются верными, а какие - неверными?
А. Узнать приблизительную глубину водных объектов можно при шкалы высот и глубин.
Б. Абсолютная высота - это превышение высоты точки над уровнем Мирового океана.
В. На физических картах зеленым цветом обычно изображают леса.
6. Каким на картах показывают глубины океанов
А. послойной окраской
Б. штриховкой
В. без цвета
7. Что такое изобаты.
А. температура воды
Б. линии, соединяющие точки с одинаковыми глубинами
В. атмосферное давление
8. Для чего на карту помещают шкалу высот и глубин.
А. позволяет расшифровать значение того или иного цвета
Б. для разнообразия цвета
В. для фона
1)
Радиус вписанной окружности правильного многоугольника совпадает с его апофемой (т.е. перпендикуляром, опущенным из центра на любую сторону)
Правильный шестиугольник можно разделить на 6 правильных треугольников. Его площадь равна площади 6 таких треугольников и S(шестиугольника)=6•S (треуг)
Нам известен радиус вписанной в шестиугольник окружности, т.е. высота правильного треугольника АОВ (см. рисунок). Для нахождения площади правильного треугольника воспользуемся формулой
Тогда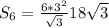 дм²
дм²
––––––––––
2)
По условию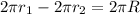
Примем коэффициент отношения радиусов окружностей равным а. Тогда радиус первой равен 5а, второй –3а
5a-3a=40⇒
a=20 см
r1=100 см=1м
S1=π•1²=π м²
60 см=0,6 м
S2=π•(0,6)²=0,36 м²
–––––––––––
3)
Найдите площадь сегмента круга, радиуса 4 см, если его хорда равна 4√2 см
Пусть центр круга О, хорда - АВ.
АО=ВО ⇒∆ АОВ - равнобедренный
По т.косинусов АВ²=АО²+ВО²- 2АО•ВО•cos∠AOB
32=2•16-2•16•cosAOB⇒
cos AOB=0, ⇒ ∠АОВ=90°.
Площадь искомого сегмента равна разности площадей сектора с углом 90° и прямоугольного ∆ АОВ.
Градусная мера полного круга 360°, значит, площадь сектора с углом 90°=1/4 площади круга
S сектора=16π:4=4π
S ∆ АОВ=4•4:2=4•2
S сегм=4π-4•2=4(π-2)= ≈4,566 см²
4)
Отношения отрезков сторон треугольника АВС, на которые их делят данные точки, одинаковы.
Примем коэффициент отношения отрезков сторон равным а.
Тогда АВ=7а.
Треугольники у вершин подобны треугольнику АВС, т.к. имеют общую вершину и стороны исходного треугольника пропорциональны сторонам треугольников, «отсекаемых» от него у вершин, с коэффициентом подобия 7:2, Поэтому эти отсекаемые треугольники равновелики.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k=АВ:ВК=7:2 ⇒
S (ABC):S(BKM)=k²= 49/4
245:S(BKM)=49:4⇒
S(Δ BKM)=20
S(ТКМОНР)=245-3•20=185 мм²