Медианы треугольника пересекаются в одной точке.
Высоты треугольника пересекаются в одной точке.
В данном треугольнике эти точки совпадают - медианы являются также высотами.
Совпадение медианы и высоты к основанию - признак равнобедренного треугольника.
Таким образом данный треугольник является равнобедренным относительно любой стороны, то есть равносторонним.
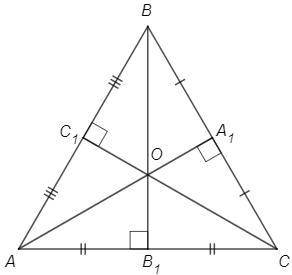
O - точка пересечения медиан, AA1 - медиана, A1 - середина BC.
O - точка пересечения высот (ортоцентр), AA1 проходит через точку O => AA1 - высота, AA1⊥BC
∠AA1B=∠AA1C=90 (AA1 - высота)
BA1=CA1 (AA1 - медиана)
△BAA1=△CAA1 (по двум катетам, AA1 - общий) => AB=AC
(Доказали: Если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.)
Аналогично: BB1 - медиана и высота к стороне AC => AB=BC
AB=AC=BC, △ABC - равносторонний
ответь:
1. Уравнение прямой AM, параллельной стороне ВС.
Вектор ВС = (1-(-1); -3-2) = (2; -5). Угловой коэффициент к = -5/2.
У прямой АМ "к" тоже равен (-5/2).
Уравнение AM: y = (-5/2)x + в. Для определения в подставим координаты точки А: -3 = 5*(-5/2) + B, отсюда в = -3+ (25/2) = 19/2.
Получаем уравнение AM: y = (-5/2)x + (19/2).
2. Уравнение медианы ВК;
Находим координаты точки К как середину Ас
K((5+1)/2; (-3-3)/2) = (3; -3). Вектор ВК =
= (4;
-5), K = -5/4.
BK: y = (-5/4)x +в, вставим точку В: 2 = (-5/4)*(-1) + B, B = 2 -(5/4)= 3/4.
Уравнение ВК: y = -1,25x+ 0,753. Уравнение высоты, проведенной через вершину А;
Это перпендикуляр к стороне ВС: к = -1/(-5/2) = 2/5.
уравнение: у = (2/5)x + в, вставим точку A(5;-3):
-3 = (2/5)*5 + в, в = - -3-2 =-5. Уравнение:
y = (2/5)x - 5.
4. Угол В; векторы ВА и ВС:
BA(6; -5), модуль √(36+25) = √61.
BC(2; -5), модуль √(4+25) = √29.
cos a = (6*2 + (-5)*(-5))/(v/61*v/29) = 37/ √(61*29) 0,879706514
B = 0,495551673 радиан
в = 28,39301942 градусов
5. Координаты точки пересечения медиан треугольника ABC.
Координаты центроида (точка пересечения медиан): М(Хм;Ум) ((Ха+Хв+Хc)/3; (Уа+Ув+Ус)/3) = (1,6667;-1,3333
).
ну, я вижу, с параллельностью не все гладко
1. важнее всего доказать, что если внутренние накрест лежащие углы равны, то прямые параллельны. То есть обратную теорему. Это делается от противного. А имено, предполагается, что две прямые АС и BD пересекают третью прямую в точках А и C, и при этом НЕ параллельны. То есть где то пересекаются, пусть в точке О. Образуется треугольник АСО. Можно построить равный ему треугольник АСО1, так, что вершина О1 лежит в другой, нежели точка O, полуплоскости. Из равенства этих треугольников следует, что угол ОАС = угол О1СА; угол О1АС = угол ОСА; и по условию угол ОАС = угол АСD. Получается, О, С и О1 лежат на одной прямой, поскольку СО1 является продолжением ОС. Но точно так же можно показать, что и точки О, А и О1 лежат на одной прямой. Получилось, что через две точки (точки О и О1) мы провели две разных прямых (одна проходит через А, другая - через С), а это противоречит аксиоме геометрии. Это доказывает, что ЕСЛИ внутренние накрест лежащие углы равны, ТО прямые параллельны.
Отсюда следует, что две прямые, перпендикулярные третьей, параллельны.
2. Обратное утверждение, заданное в задаче, доказывается с использованием теоремы пункта 1.
Если две прямые параллельны, а внутренние накрест лежащие углы НЕ равны (предположим, что это так), то через точку пересечения первой прямой с секущей проведем прямую так, чтобы внутренний накрест лежащий угол был равен с углом, образованным второй прямой.
Но из пункта 1. мы знаем, что построенная прямая параллельна второй прямой. То есть получилось, что через одну точку проходят две прямые, параллельные одной прямой. Противоречие, которое доказывает утверждение задачи.