
Объяснение:
Сумма острых углов в прямоугольном треугольнике равна 90°
1) <B=90°-<А=90°-36°=54°
ответ: <В=54°
2) Сумма острых углов в прямоугольном треугольнике равна 180°
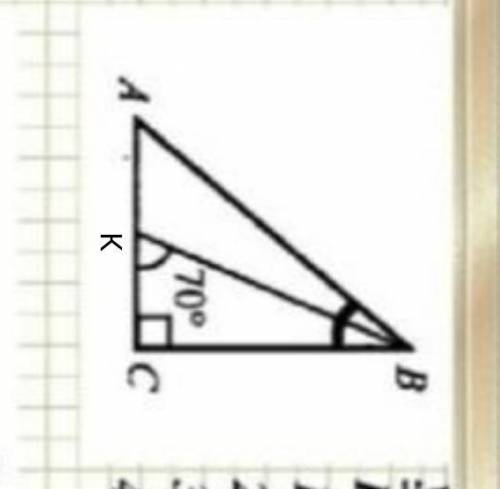
<СВК=90°-70°=20°
ВК- биссектрисса
<СВА=2*<СВК=2*40°=80°
Сумма острых углов в прямоугольном треугольнике равна 90°
<САВ=90°-<СВА=90°-80°=10°
ответ: <САВ=10°
3) ВС- катет против угла 30°
ВС=1/2*АВ=15/2=7,5см
ответ: ВС=7,5см
4)
Катет ВС равен половине гипотенузы АС. В том случае когда лежит против угла 30°
Угол <А=30°.
Сумма острых углов в прямоугольном треугольнике равна 90°
<С=90°-30°=60°
ответ: <А=30°; <С=60°
"1. На луче с началом в точке А отмечены точки В и С. Известно, что AC = 7, 8см, ВС = 2,5 см. Какую длину может иметь отрезок АВ?
2. Луч BP проходит между сторонами угла ABC. Найдите угол РВС, Если угол ABC равен 83 , угол АВР равна 48
3. Один из двух углов, образованных при пересечении двух прямых, на 22 меньше второго. Найдите все образовавшиеся углы.
4. Один из смежных углов в 4 раза меньше второго. "
1) АВ=АС-ВС.
АВ=7,8-2,5=5,3 см.
2) ∠РВС=∠АВС-∠АВР=83*-48*=35*.
3) Меньший угол обозначим через х. Тогда больший будет х+22*
Эти углы смежные и их сумма равна 180*.
х+х+22*=180*.
2х=158*.
х=79*. - меньший угол.
79*+22*=101* - больший угол.
ответ: При пересечении двух прямых образовалось четыре угла: два смежных 79* и 100* и два накрест лежащих: 79*=79* и 101*=101*.
4) меньший угол обозначим через х. Тогда больший будет 4х. Сумма смежных углов равна 180*.
х+4х=180*.
5х=180*.
х=36* - меньший угол.
Больший угол равен 36*4=144*
ответ: 36* и 144*( 36*+144*=180*)
№1
№1Дано:
ABCD – параллелограмм,
DE – высота, равная 4,
CD=8.
Найти: S(ABCD)
Найти: S(ABCD)Решение:
S=a*h, где S – площадь параллелограмма, а – сторона параллелограмма, h – высота параллелограмма, проведенная к этой стороне.
Противоположные стороны параллелограмма равны, следовательно AB=CD=8.
S=AB*DE=8*4=32.
ответ: 32.
№2
Дано:
ABCD – параллелограмм,
BD – высота и диагональ параллелограмма, равная 13,
AD=12
Найти: S(ABCD)
S=a*h, где S – площадь параллелограмма, а – сторона параллелограмма, h – высота параллелограмма, проведенная к этой стороне.
S=AD*BD=12*13=156.
ответ: 156.
№3
Дано:
ABCD – параллелограмм,
ВН – высота, равная 5,
AH=12,
AB=13,
HD=3.
Найти: S(ABCD)
S=a*h, где S – площадь параллелограмма, а – сторона параллелограмма, h – высота параллелограмма, проведенная к этой стороне.
S=AD*BH=(AH+HD)*BH=(12+3)*5=15*5=75.
ответ: 75.