Сторона основания а = √64 = 8, половина диагонали основания АО = 4√2.
Так как отрезок КО лежит в плоскости DPO, перпендикулярной плоскости основания, в том числе и диагонали АС, то угол КОА равен 90 градусов.
Находим КО = АО*ctg(AKO) = 4√2*(√10/4) = √2*√10 = 2√5.
Так как КО - это медиана из прямого угла к гипотенузе, то гипотенуза (а это боковое ребро) равна двум медианам.
Значит, боковое ребро L равно 2*(2√5) = 4√5.
Высота пирамиды H = √(L² - (a/2)²) = √(16*5 - 16) = 8.
Апофема А = √(Н² + (а/2)²) = √(64 + 16) = √80 = 4√5.
Площадь боковой поверхности Sбок = (1/2)РА = (1/2)*(8*4)*4√5 = 64√5.
Площадь поверхности S = So + Sбок = 64 + 64√5 = 64(1 + √5).

Объяснение:
Найдем угол А: 90 - 27 = 63 градуса(сумма острых углов в прямоугольном треугольнике равна 90 градусов).
Найдем гипотенузу AB.
Синус угла A равен отношению противолежащего данному углу катета BC к гипотенузе AB.
Иначе говоря:
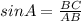
Синус 63 градусов равен 0,891007.
Выразим из этой формулы AB:
AB = BC/sinA = 13/0,891007 = 14,6
Для того, чтобы найти катет AC, мы должны использовать тангенс, т.к. именно эта тригонометрическая функция связывает оба катета.

Тангенс - это отношение противолежащего катета к прилежащему.
Тангенс 27 градусов равен 0,21.
Чтобы найти AC, мы тангенс угла B умножим на BC.
AC = tgB * BC = 0,51 * 13 = 6,63
r = 2см.
Объяснение:
Есть формула для ЛЮБОГО треугольника: S = p*r, где S - площадь треугольника, p - его полупериметр, r - радиус вписанной окружности.
В нашем случае S = (1/2)6*8 = 24cм².
р = (6+8+10):2 = 12 см.
r = 24/12 = 2 см.