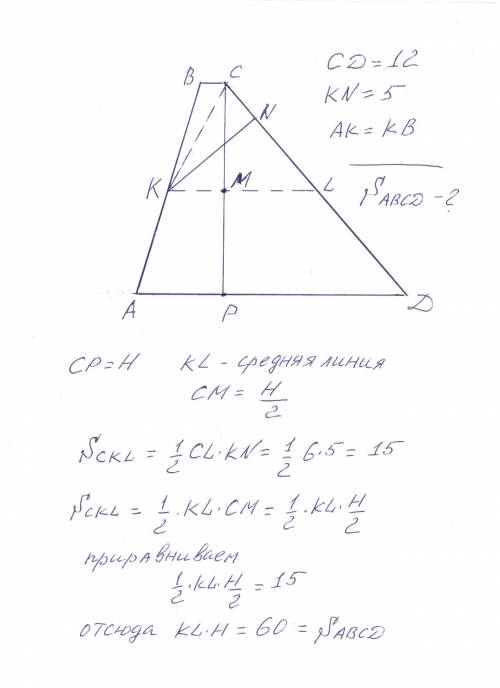
Через точку К проведём прямую КL параллельно АД. То есть КL-это средняя линия трапеции АВСД, далее смотри рисунок.
остроугольный и равнобедренный.
Объяснение:
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
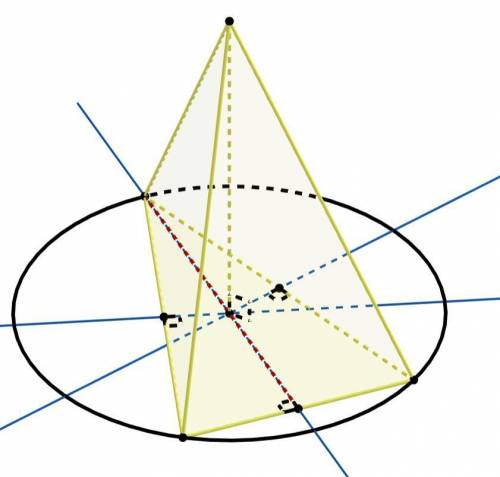
остроугольный и равнобедренный.
Объяснение:
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.

См. Чертеж.
Треугольники ЕВС и МАЕ равны (ЕА = ЕВ, и углы ЕВС и ЕАМ, и МЕА и ВЕС - попарно равны). Поэтому МА = ВС. Расстояние от Е до АD равно половине высоты трапеции, а МD равно сумме оснований. Поэтому площадь треугольника MDE равна половине площади трапеции. но площадь МDE равна сумме площадей ВЕС и АЕD. Получается, что площадь треугольника CED равна половине площади трапеции ABCD.
Площадь CED равна (1/2)*ЕК*СD, поэтому площадь трапеции
S = EK*CD = 5*12 = 60