
Sкруга=4n
ВС=?
Sкруга=n×r^2
4n=n×r^2
r^2=4n/n=4
r=корень4=2 (ед)
NO=r=2 (ед)
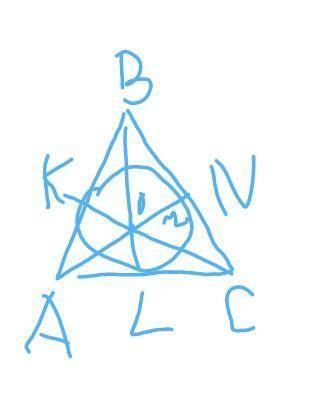
Центром окружности является точка пересечения биссектрис. В равностороннем тр-ке биссектриса является медианой и высотой.
В равностороннем тр-ке углы равны 60 градусов.
Рассмотрим тр-к ВОN:
<OBN=<ABC:2=60:2=30 градусов, т. к ВL - биссектриса.
Катет лежащий против угла 30 равен половине гипотенузе :
ВО=2×NO=2×2=4(ед)
По теореме Пифагора :
ВN=корень(ВО^2-NO^2)=
=корень (4^2-2^2)=корень(16-4)=
=корень 12=2корень3(ед)
ВС=2×ВN=2×2корень3 =4корень3 (ед)
ответ : 4корень3 (ед)
1.
Синус угла A — равен: AB/CB.
Так как угол нам уже известен(42°), то его синус найдём по таблице: 0,6691.
Тоесть — катет CB равен: 0.6691*8 = 5.353.
Катет AC — найдём по теореме Пифагора: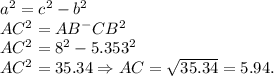
Вывод: AC = 5.94; CB = 5.353.
2.
Второй катет равен(по теореме Пифагора):
Второй катет равен: 12.7.
Найдём углы по их тангенсам.
Тангенс угла А равен: противоположный катет делить на прилежащий катет.
У нас есть треугольник ABC(прямой угол — C), по нашим расчётам — AB = 15; AC = 8; BC = 12.7.
Вывод: <B = 33°; <A = 57°.
3.
<M = 70° => <K = 90-70 = 20°.
Формула вычисления катета, зная гипотенузу, и угол прилежащего катета таков:
Гипотенузу найдём по теореме Пифагора: