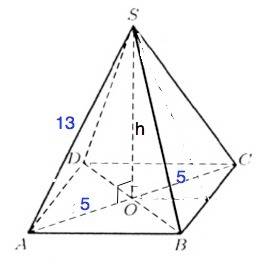
Диагональ основания правильной четырехугольной пирамиды равна 10 см, а боковое ребро 13 см. Найти площадь диагонального сечения пирамиды.
Основанием правильной четырехугольной пирамиды является квадрат, а вершина пирамиды проецируется в его центр, т.е. точку пересечения его диагоналей. .
Следовательно, высота ЅО принадлежит диагональному сечению АЅС пирамиды.
Пусть дана пирамида SABCD, SO -её высота. Диагонали основания равны, точкой пересечения делятся пополам, а диагональные сечения - равные равнобедренные треугольники.
Высота ЅО перпендикулярна основанию и любой прямой, на плоскости АВСD. =>
∆ АОЅ - прямоугольный.
По т.Пифагора ЅО=√(SA²-AO²)=√(169-25)=12см
S(ASC)=SO•AC:2=12•5=60 см²
Відповідь:
120°
Пояснення:
Дано: ΔАВС- рівнобедрений, АВ=ВС=29,2 см, АК⊥АС, АК=14,6 см.
Знайти: ∠- найбільший.
Рішення: Зна ємо, що найбільший кут лежить проти більшої сторони.
Розглянемо ΔАВК, ∠К=90°, АВ=29,2 см, АК=14,6 см.
В ΔАКВ sin ∠A=14,6/29,2=1/2 . Отже ∠А=30°.
За теоремою про суму гострих кутів прямокутного трикутника
∠АВК=90-30°=60°.
За властивістю висоти рівнобедреного трикутника, що проведена до його основи АК є бісектрисою кута В ΔАВС.
Тому ∠В=2* ∠АВК=2*60°=120°
В- найбільший