51 см или 57 см.
Объяснение:
Треугольник равнобедренный, а значит какие-то две стороны равны. Либо две стороны равны 15 см, либо две стороны равны 21 см.
Но существует неравенство треугольника, из которого следует, что одна из сторон обязана быть меньше, чем сумма двух других.
То есть в треугольнике АВС: АС < АВ+ВС; АВ < АС+ВС; ВС < АВ+АС
Проверим, какой равнобедренный треугольник с представленными сторонами может существовать:
Допустим АВ = 15 см, АС = 21 см, а ВС = 15 см.
Тогда АВ < АС+ВС (15 < 21+15 - верно), АС < АВ+ВС (21 < 15+15 - верно),
ВС < АВ+АС (15 < 15+21 - верно)
Такой треугольник может существовать.
Проверим второй вариант:
АВ = 15 см, АС = 21 см, а ВС = 21 см.
Тогда АВ < АС+ВС (15 < 21+21 - верно), АС < АВ+ВС (21 < 15+21 - верно),
ВС < АВ+АС (21 < 15+21 - верно)
И такой треугольник может существовать.
Ну а теперь найдем два варианта периметра этого треугольника (периметр - это сумма всех его сторон).
Периметр 1: 15см+21см+15см = 51см.
Периметр 2: 15+21см+21см = 57 см.
Смотрите, что надо сделать, чтобы решение само по себе возникло:)))
Пусть треугольник АВС, АС - основание, АВ = ВС;
Ясно, что если внешний угол 60, то внутренний 120, и это угол при вершине, а углы при основании равны 60/2 = 30 градусов.
(Не может быть 120 - угол при основании :))- это я так, на всякий случай.)
Продлите сторону СВ за вершину В, и из точки А проведите перпендикуляр к этой прямой. Пусть точка пересечения К. Тогда треугольник КАС - прямоугольный, в нем известен острый угол КСА = 30 градусов, и катет АК = 17 :))) А найти надо гипотенузу АС. Поэтому ответ 34 :)))
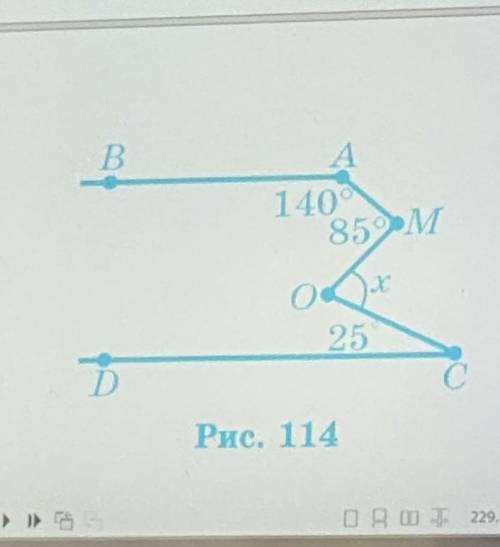
СОМ = 80
140-(25-85)=80