Существует несколько решения такой задачи. В архиве есть два, одно из них мое же, но там задача с несколько иным условием и решена иначе, при желании без труда найдете их.
Вот еще один:
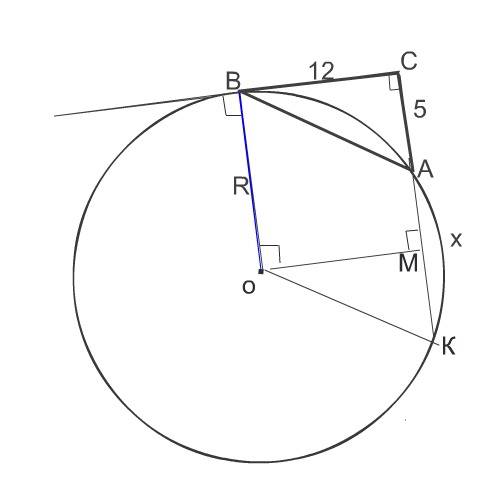
См. рисунок.
Воспользуемся теоремой:
Если из точки вне окружности к ней проведены касательная и секущая, то
квадрат длины отрезка касательной равен произведению всего отрезка секущей к его внешней части.
ВС²=АС*СК
144=5 *(5+х)
144=25 +5х
5х =144-25=119
х=23,8
Проведем перпендикуляры ОВ к точке касания В и ОМ к хорде АК.
Так как треугольник АВС прямоугольный, то ОМ║и =ВС, ОВ║ и=МС
Радиус равен ОВ=МС
Перпендикуляр из центра окружности к хорде делит ее пополам.
R=CК-АК:2=СК-МК
СК=5+23,8=28,8
МК=23,8 :2=11,9
R=28,8-11,9=16,9
ответ: Радиус равен 16,9
Средняя линия треугольника параллельна его третьей стороне и равна ее половине.
5.
1) КН║АС, КН = АС/2 как средняя линия треугольника АВС,
МР║АС, МР = АС/2 как средняя линия треугольника ADC, значит
КН║МР и КН = МР, а если противоположные стороны четырехугольника параллельны и равны, то это параллелограмм.
КНРМ - параллелограмм.
2) Аналогично доказываем, что КНРМ параллелограмм и добавим, что
НР = KM = BD/2 (как средние линии соответствующих треугольников)
КН = МР = АС/2.
В прямоугольнике диагонали равны, значит стороны параллелограмма КНРМ равны, и следовательно это ромб.
3) Все то же и
КН║МР║АС, КМ║НР║BD.
Диагонали ромба перпендикулярны, значит и смежные стороны параллелограмма КНРМ перпендикулярны, и следовательно, это прямоугольник.
4) Так как квадрат - это прямоугольник с равными сторонами, то из задач 2) и 3) следует, что КНРМ - ромб с перпендикулярными смежными сторонами, то есть квадрат.
6. По свойству средней линии треугольника:
КН = АС/2 = 15/2 = 7,5 см
НР = АВ/2 = 10/2 = 5 см
КР = ВС/2 = 12/2 = 6 см