Диагональ нижнего основания пирамиды l1 равно
(l1)^2=8^2+8^2=128
l1=8*sqrt(2)
Диагональ верхнего основания пирамиды l2 равно
(l2)^2=6^2+6^2=72
l2=6*sqrt(2)
Половина нижней диагонали равна 4*sqrt(2), а половина верхней 3*sqrt(2)
Их разность равна 4*sqrt(2)- 3*sqrt(2)=sqrt(2)
Рассмотрим прямоугольный треугольник, стороны которого равны sqrt(2) и высота пирамиды - это катеты, а гипотенуза - боковое ребро пирамиды (n), тогда
n^2=5^2+(sqrt(2)^2=25+2=27
n=sqrt(27) - боковое ребро пирамиды
Объяснение:
Объяснение:
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.
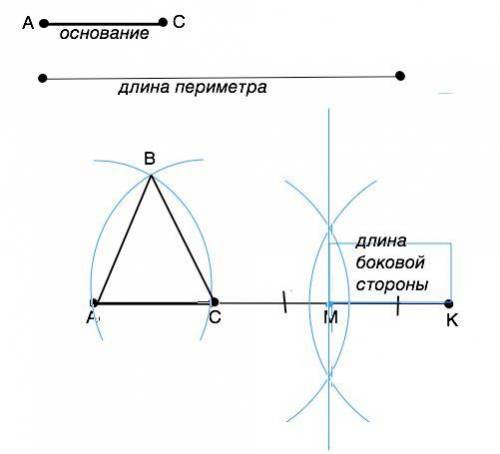
Решение заданий во вложении))