

такого треугольника не существует
или 60 см^2.
Объяснение:
Треугольника с заданными сторонами не существует.
13 см > 10см + 13мм, не выполнено неравенство для сторон треугольника.
Если в условии опечатка, длины стороны треугольника 13 см, 13 см, 10 см, то площадь может быть найдена по формуле Герона:
S = √p•(p-a)•(p-b)•(p-c).
p = (10+13+13):2 = 18 (см),
S = √18•(18-13)•(18-13)•(18-10) = √(18•5^2•8) = √(9•5^2•16) = 3•5•4 = 60 (см^2)
Ещё одним может быть нахождение по формуле
S = 1/2•a•h, где а = 10 см, а длина высоты найдена по теореме Пифагора из прямоугольного треугольника, образованного боковой стороной, высотой, проведённой к основанию, и половиной основания, h = 12 см.
(S = 1/2•10•12 = 60 (см^2) ).
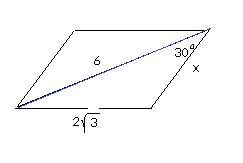
Пусть будет треу-к АВС, где ВС=АС – боковые стороны и АВ – основание. Тогда СМ– медиана. Но медиана проведенная к основанию является и высотой. Тогда СМ перпендикулярен АВ. Тогда по теореме Пифагора: АМ^2=28; АМ=2sqrt7. Тогда АВ=2АМ=4sqrt7. ответ: 4sqrt7(sqrt – корень квадратный, если вдруг не знаешь)
Удачи.
Добавил решение, если медиана проведена к боковой стороне. Там надо достроить до параллелограмма или к треугольнику АВС достроить треугольник DCB с общей стороной ВС, и тогда все равно получится параллелограм. Все написал во вложениях.