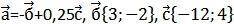

ответ: после построения диагоналей ромб разбивается на 4 треугольника. диагонали ромба располагаются под прямым углом, то есть, треугольники, которые образовались, оказываются прямоугольными.
обозначим большую и малую диагонали ромба как d₁ и d₂, а углы ромба — а (острый) и в (тупой), теперь из формулы
tg a = 2/((d₁/d₂)-(d₂/d₁)) находим
tg a = 2/((2√3 /2)-(2/2√3)) = 2/(√3-1/√3)=
2/(√3-√3/3=2/(√3(1-1/3)= 2/(√3(2/3)=
2√3/2=√3
tg 60°=√3
углы ромба 60° и 120°
подробнее - на -
объяснение:
Объяснение:
a=-b+1/2c=-(3;-2)+1/2*(-6;2)=(-3;-(-2))+(1/2*(-6);1/2*2)=(-3;2)+(-3;1)=(-3+(-3);2+1)=(-6;3)
\begin{gathered}|a|=\sqrt{(-6)^2+3^2}=\sqrt{36+9}=\sqrt{45}=sqrt{9*5}=\sqrt{9}*\sqrt{5}=3\sqrt{5}\end{gathered}
∣a∣=
(−6)
2
+3
2
=
36+9
=
45
=
9∗5
=
9
∗
5
=3
5