1)Найдите площадь треугольника, две стороны которого равны 2√3 и 23, а угол между ними равен 60° 2) Угол при вершине остроугольного треугольника равен 150°. Найдите боковую сторону треугольника, если если его площадь равна 2.25
3) Площадь треугольника АВС равна 11 DE средняя линия. Найдите площадь треугольника CDE.
4) найдите периметр прямоугольника, если его площадь равна 135, а отношения соседний сторон равна 3:5

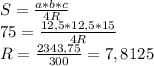
В треугольнике, образованном высотой, проведенной к основанию, боковой стороной и половиной основания (данный нам треугольник равнобедренный) биссектриса угла при основании делит эту высоту в отношении 5:4, значит по свойству биссектрисы: "Биссектриса делит сторону, противолежащую углу в отношении сторон, образующих данный угол", имеем: (Х-9)/(Х/2)=5/4 или (9-Х)*2/Х=5/4. Тогда 8Х-72=5Х, отсюда Х=24. Итак, по Пифагору искомая высота равна
√[(Х-9)²-(X/2)²]=√(15²-12²)=9см.
ответ: высота, проведенная к основанию, равна 9см.