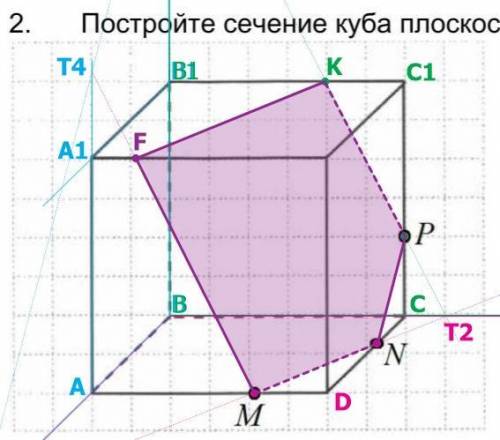
ответ: на рисунке))
Объяснение:
прямые, лежащие в одной плоскости, либо параллельны,
либо пересекаются... сечение -многоугольник, вершины которого лежат на ребрах многогранника, стороны которого принадлежат граням многогранника -это линии пересечения плоскости сечения с плоскостями-гранями...
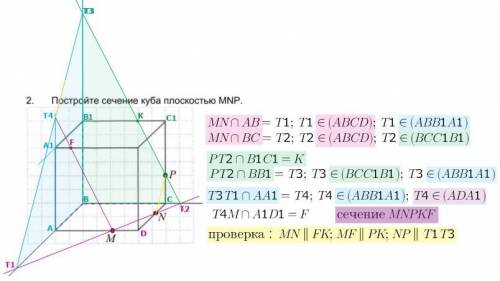
по условию заданы прямые MN∈(ABCD) и NP∈(CDD1C1);
MN может пересечься с прямыми, лежащими в плоскости (ABCD):
это АВ (которая принадлежит и плоскости (ABB1A1))
и ВС (которая принадлежит и плоскости (BCC1B1))...
результат построения можно проверить по теореме: две параллельные плоскости при пересечении с третьей плоскостью (сечением) дадут параллельные линии пересечения...
OC ⊥ BM ( OC ⊥ BC ,где O центр малой окружности , BC касательная) ⇒ AM | | OC . MC/CB= AO/OB (обобщенная теорема Фалеса) .
2,4 /4 =r/(2R -r) ⇔ r=3R/4 (1) .
Из ΔBCO по теореме Пифагора :
OB² - OC² =BC² ;
(2R -r)² - r² = 4² ⇔ 4R(R-r) =16 ⇔ R(R-r) =4 (2).
R(R -3R/4) =4 ⇒ R =4. ⇒ r=3R/4 = 3.
AD =AC+CD.
AM =√(AB² -BM²) =√((2R)² -(MC+CB)² ) =√(8² -6,4²) =√(8 -6,4)(8 +6,4) =4,8.
AM можно вычислить по другому: AM/OC =MB/CB ⇔ AM/3 =6,4/4⇒
AM =4,8.
---
AC =√(BC² +AM²) =√(2,4² +4,8²) =√(2,4² +(2*2,4)²) = 2,4√5.
AC*CD = MC*BC ⇔ 2,4√5 *CD =2,4*4⇒ CD =4/√5 =4√5 / 5 =0,8√5.
AD =AC+CD= 2,4√5 + 0,8√5 =3,2√5 .