Точка касания окружности вписанной в равнобедренную трапецию делит ее боковую сторону на отрезки длиной 9 см и 16 см. Найдите площадь трапеции
Объяснение:
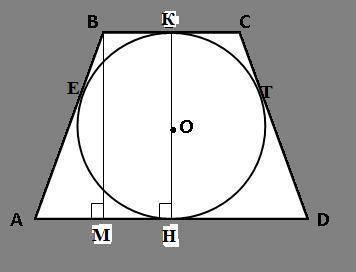
АВСD-трапеция АВ=СD, точки касания расположены на сторонах
А-Е-В, В-К-С, С-Т-D, А-Н-D ,АЕ=16 см, ЕВ=9 см.
АВ=16+9=25 см. Значит СD=25 см.
S(трап.)= 1/2*Р*r , r-радиус вписанной окружности .
По свойству отрезков касательных АЕ=АН=DT=DH=16 см и
ВК=ВЕ=СК=СТ=9 см.
Р=25+25+(9+9)+(16+16)=100 (см)
Радиус вписаной окружности равен половинге высоты трапеции.
Пусть ВМ⊥АD ,ΔАВМ-прямоугольный , по т. Пифагора ВМ=√(25²-7²)=√576=24 (см)
Тогда r=1/2*24=12(см).
S(трап.)=1/2*100*12=600 (см²)
Треугольник ВАD - прямоугольный, так как ВD - диаметр, а угол ВАД опирается на диаметр и потому - прямой.
ВС=1/2 АВ, поэтому угол ВАС=30 градусов, а АВС=60 градусов. Соответственно, и угол АDВ=30 градусов.
Углы в треугольнике ВАО все равны 60 градусов,
дуга АВ=60 градусов.
Дуга АD=120 градусов,
Что такое дуга ВС и дуга СD - не поняла, так как С не принадлежит окружности и .
эти отрезки дугами не являются.