Эта задача на много проще, чем кажется. Если из центра окружности (который лежит на гипотенузе) опустить перпендикуляры на катеты, то получится квадрат и два треугольника, подобных исходному. Если обозначить радиус окружности r, больший катет большего треугольника b, меньший катет меньшего треугольника a, то стороны исходного треугольника будут такие (a + r, b + r, 35) стороны меньшего треугольника (a, r, 15) стороны большего (r, b, 20) и все эти три треугольника подобны между собой. отсюда a/r = 15/20 = 3/4; то есть все эти три треугольника - египетские (подобные треугольнику со сторонами 3, 4, 5) То есть уже можно написать ответ :) вычислять уже ничего не надо, надо просто "подобрать" коэффициенты подобия, чтобы гипотенузы египетских треугольников были бы 15 и 20. Само собой, это 3 и 4. То есть a = 9, r = 12, b = 16; (получились треугольники 9, 12, 15 и 12, 16, 20) Исходный треугольник имеет стороны 21, 28, 35, его площадь 294; длина полуокружности πr = 12π;
Весь "трюк" в том, что r - одновременно больший катет в одном из подобных треугольников и меньший - в другом.
Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3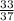 ,AD=37-3
,AD=37-3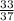 =33
=33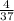
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD=3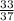 *33
*33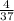 =
=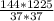 , CD=√(
, CD=√(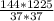 )=12*35/37=420/37
)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10