Вообщем я немного упростила это решение
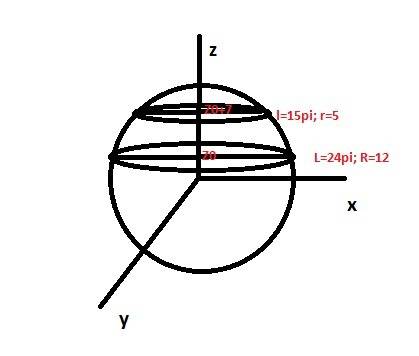
Пусть большее сечение лежит выше центра шара по оси Z , его радиус 12 и центр в точке (0;0;z0)
Тогда его уравнение будет x^2+y^2+z0^2=R^2
Здесь R радиус сферы. Так как радиус большего сечения 12(24pi/2pi), то уравнение большего круга
Будет 12^2+z0^2=R^2
Меньшее сечение x^2+y^2+(z0+7)^2==R^2; 25+z0^2+14z0+47=R^2
Вычитаю из первого второе , получу
119-17z0-49=0
-14z0=-70
Z0=5
Выходит большее сечение находится от центра шара по оси z на расстоянии 5, значит
R^2=5^2+12^2=169
R=13
S(cф)=4pi*13^2=676pi
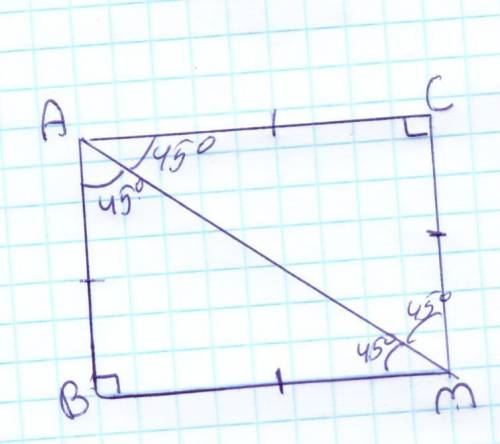
так как K L M N являются серединами,то AK=KB=BL=LC=CM=CD, а AN=ND
если угол А =40 градусов, то кгол В=180-40=140, при этом угол А=углу D, а угол В=углу С
треугольник BKL-равнобедренный,потому что BL=BK, поэтому глы у остнования этого треугольника по 20 градусов, следовательно у треугольника LCM градусные меры углов такие же
тогда угол KLM=180-(20+20)=140 градусов
KLMN явл параллелограмом, поэтому чамый большой гол равен 140