


1) 80*, 80*.
2) 30*, 50*.
3) с<9.4; c=9.3 см.
Объяснение:
1) Треугольник равнобедренный и углы при основании равны.
Угол А равен углу В равен (180*-20*)/2 = 160*/2 = 80*.
***
Угол Р=30*; 180*-60*-90*=30*;
Угол С=180*-90*-40 = 50*;
***
Условие существования треугольника a+b>c;
a+b=7.1+2.3=9.4. Значит с<9.4. Например с=9,3 см.
Искомую площадь можно найти по-разному.
1) Найти площадь четырехугольника АВОС и из нее вычесть площадь сектора круга.
2) Найти площадь ∆ АВС и из неё вычесть площадь сегмента. ограниченного дугой ВС и хордой ВС.
1) Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности⇒
∠ВАО=∠САО=120°:2=60°
∠АВО=∠АСО=90° т.к. радиусы, проведенные в точки касания, перпендикулярны касательным. ⇒
угол ВОС=60°, и ∆ ВОС - равносторонний.
∆ АВО=∆ АСО - прямоугольные.
АВ=BО:tg60°=6/√3=2√3
Длина дуги ВС =1/6 длины окружности, т.к. угол ВОС=1/6 полного круга.
◡ВС=2πr:6=12π:6=2π
P=AB+AC+◡BC=2•2√3+2π=4√3+2π = ≈13,2114 см
Ѕ (АВОС)=2Ѕ(АВО)=ВО•AB=6•2√3=12√3
S (сектора)=1/6πr²=36π:6=6π
S(фиг. АВС)=S(ABOC)-S(сект)=12√3-6π=6•(2√3-π)=≈1,935 см*
Объяснение:
Как то так))) надеюсь удачки))
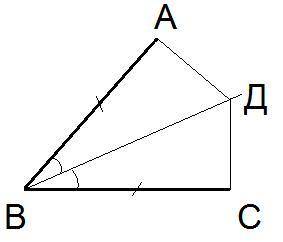
ответ: Периметр четырехугольника АВСД= 31 см
Объяснение: См. рисунок.
1) Равны треугольники АВД и ДСВ. В этих треугольниках имеются равные углы <ДВА и <ДВС., так как ВД - биссектриса. Так же имеются две равные стороны: ВА и ВС (по условию), и общая сторона ДВ. Таким образом, ΔАВД=ΔДВС по двум сторонам и углы между ними (первый признак равенства треугольников)
Сторона ВС ΔВСД = стороне АВ ΔАДВ;
Сторона ДС ΔВСД = стороне АД ΔАДВ;
Сторона ДВ ΔВСД = стороне ВД ΔАДВ;
Угол ДВС ΔВСД = углу ДВА ΔАДВ;
2) Выше было показано, что ДС = АД = 5,7 см. Тогда периметр четырехугольника АВСД = АВ + ВС + СД + АД = 9,8 + 9,8 + 5,7 + 5,7 = 31 см.
ответ: для первой фотки
A=80
B=80
Объяснение:
так как стороны AC и CB равны треугольник равнобедренный , у равнобедренного треугольника углы у основания равны
сумма углов любого треугольника равна 180 градусов.
180-20=160
160:2 =80
ответ для второй фотки: