Объяснение:
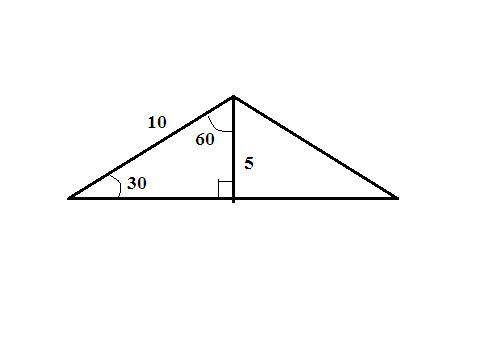
1. находим боковые стороны равнобедренного треугольника через его площадь:
S=a²sin120°/2 ⇒ a²=(25√3)/(√3/2)/2=25*4, a=√(25*4)=5*2=10 см - боковые стороны.
2. находим основание:
высота, проведенная к основанию равнобедренного треугольника, образует с боковой стороной и половиной основания прямоугольный треугольник где гипотенуза - боковая сторона - 10 см. Углы в этом треугольнике 90°, 60°, 30°. Против угла 30° (высота треугольника) лежит катет в два раза меньше гипотенузы ⇒ высота - 10/2=5 см;
далее либо по т. Пифагора находим половину основания треугольника, либо через формулу нахождения площади находим длину всего основания.
т. Пифагора: √(10²-5²)=√75=5√3 см - половина основания, (5√3)*2=10√3 - основание треугольника;
через площадь: в*h/2=25√3, в=50√3/5=10√3 см.
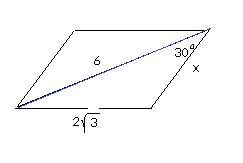


Площадь ромба равна S=1/2(дробью) * на диагональ(1) * диагональ(2). Для решения нужно найти вторую диагональ. Она равна Рассмотррим прямоугольный тругольник Катет(1) равен 84/2=42, гипотенуза=58, По теореме пифагора сумма квадрата катетов равна квадрату гипотенузы, отсюда второй катет( половины второй диагонали) равна (58) в квадрате - (42) в квадрате)=1600=40. Вторая диагональ равна 40*2=80. Площадь равна 3360