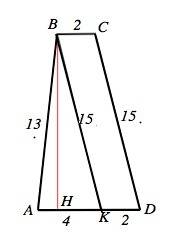
Обозначим трапецию АВСD.
АВ=13 см, СD=15 см, ВС=2 см, AD=6 см. ВН - высота трапеции.
Через вершину В проведем ВК параллельно СD.
Противоположные стороны четырехугольника КВСD параллельны – КВСD - параллелограмм, KD=ВС=2 см
Тогда АК=4 см.
Площадь ∆ АВК по ф. Герона , где р - полупериметр,
равна √(p•(p-AB)•(p-BK)•(p-AK)=√16•3•1•12)=24 см²
ВН =высота трапеции=высота ∆ АВК.
Из формулы площади треугольника
h=2S:a, где а- сторона, к которой высота проведена.
ВН=48:4=12 (см)
Площадь трапеции равна произведению высоты на полусумму оснований.
S(ABCD)=12•(2+6):2=48 см*
1. Найдем катеты прямоугольного треугольника. Пусть x - 1 часть. Тогда 3х - 1 катет, 4х - второй катет. Решая уравнение по т. Пифагора, получим: 9x^2+16x^2=2500
25x^2=2500
x^2=100
x=-+10
-10 мы значение не берем по смыслу. Значит, x=10.
Тогда 3х = 3*10 = 30(мм)
4х = 4*10 = 40(мм).
2. Если катет есть среднее пропорциональное для отрезка, делящаяся высотой, проведенной из вершины угла, и гипотенузы, то выразим сам этот отрезок:
ac=a^2\c
a - катет
с - гипотенуза
a с индексом с - отрезок.
ac=900\50=18
А второй отрезок можем найти разностью между гипотенузой и этим отрезком: 50-18=32(мм).
ответ: 18 и 32 мм