1) За x примем скорость течения реки, тогда
x+12км/ч-скорость по течению, 12-xкм/ч- скорость против течения
16/(x+12)ч - время туда
16/(12-x)ч - время на обратную дорогу
40 мин = 2/3ч
16/(x+12) +16/ (12-x) + 2/3=3 2/3
(16(12-x)+16(x+12))/(x+12)*(12-x)=3
384/144-x( в квадрате)=3
384=432-3х(в квадрате)
3х(в квадрате)=48
х(в квадрате)=16
х=4.
ответ: 4км/ч
2)проведи перпендикуляр OA( по свойству радиус перпендикулярен касательно в точке касания)
угол AOD- центральный, следовательно равен дуге AD=140,
угол DOA и угол AOC - смежные( т.к. DC- диаметр, след, угол DOC - развернутый), след, угол AOC = 180-140=40
Из треугольника AOC
угол С = 180-(90+40)=50
ответ 50.
3) Треугольник BEF=DEF (EF-общая, угол BEF=DFE=90, BE=DF( т.к. треугольники ABC и ACD равны( AC- общая , углол CAD=BCA как в.н.л.у. при параллельных ВС и АД и АС секущей, а т.к. АВСД- параллелограмм, то углы А и С равны, след, углы ВАС и СДА равны)и BE=DF как соответственные
лементы, следовательно углы BFE=DEF как соответственные элементы, следовательно BF и DE параллельны.
Будем считать, что у отрезков есть начальная и конечная точки, то есть направление. Теперь у нас направленные отрезки (векторы).
Если точки расположены последовательно A_C, то имеем вектор AC.
Если точки расположены последовательно C_A, то имеем вектор -AC.
AM =1/2 AB =1/2 (AC+CB)
CK =1/2 CD =1/2 (CB+BD)
AK =AC+CK =AM+MK
AC +1/2 CB +1/2 BD = 1/2 AC +1/2 CB +MK => MK =1/2 AC +1/2 BD
1) Точки расположены последовательно A_C, B_D
MK =1/2 (AC+BD) = |5+7|/2 =6
2) Точки расположены последовательно C_A, B_D
MK =1/2 (-AC+BD) = |-5+7|/2 =1
3) Точки расположены последовательно A_C, D_B
MK =1/2 (AC-BD) = |5-7|/2 =1
4) Точки расположены последовательно C_A, D_B
MK =1/2 (-AC-BD) = |-5-7|/2 =6


Объяснение:
6) Обозначим вершины треугольника АВС. R радиус описанной окружности найдём по формуле:
R=(abс)/(4S) где abc – стороны треугольников, а S –его площадь.
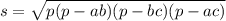
где р – полупериметр.
р=(АВ+ВС+АС)/2=(13+14+15)/2=42/2=21
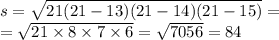
S=84(ед²)
R=(13×14×15)/(4×84)=2730/336=8,125(ед)
r=S/p – где r –радиус вписанной окружности, а р – полупериметр.
r=84/21=4(ед)
ОТВЕТ: r=4(ед); R=8,125(ед)
7) а(2; –6); b(–6; 2); c(2a+b)–?
2a=(2×2; –6×2)=(4; –12)
2a+b=(4+(–6); –12+2)=(–2; –10)
2a+b(–2; –10)
Абсолютная величина вектора 2а+b:
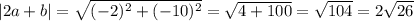
ОТВЕТ: координаты вектора 2а+b(–2; –10);
абсолютная величина вектора 2а+b=2√26
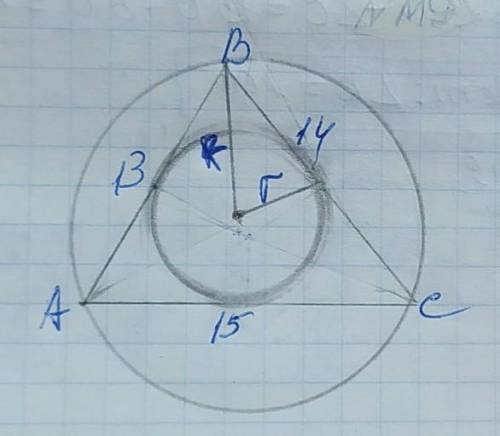
дуга AD окружности 140 градусов, значит центральный угол AOD равен 140 градусов, а смежный с ним угол AOC 180-140=40, так как АС касательная, то угол ОАС равен 90 градусов, тогда из прямоугольного треугольника АОС угол АСО=90-40=50
2) треугольник ABE = CDF, по гипотенузе и острому углу: 1) AB=CD как противолежащие стороны параллелограмма, 2) угол BAE=DCF, как внутренние накрест лежащие углы при паралельных прямых AB и CD и секущей AC,значит ВЕ=DF, AE=FC
треугольники AED=CFB по 2 сторонам и углу между ними:1) AE=FC по доказанному,2)AD=BC, как противолежащие стороны параллелограмма ABCD,3) углыEAD=FCB, как внутренние накрестлежащие при параллельных прямых AD и BC и секущей АС. Значит DE=BF. То есть АВСD-ПАРАЛЛЕЛОГРАММ, СЛЕДОВАТЕЛЬНО BF параллельна DE