12√3 СМ² или 3√3 см²
Объяснение: Используем формулу для площади четырехугольника :
S=BD*AC*sin∡BOA/2 (1)
где АС- вторая диагональ параллелограмма. О точка пересечения диагоналей.
Известно, что точка пересечения диагоналей параллелограмма делит диагонали пополам.
Тогда BO=OD=3 cm
Рассмотрим случай, когда ∡ВОА=60°
Тогда из треугольника АВО по теореме косинусов запишем
ВА²=BO²+AO²-2*BO*AO*cos∡BOA
13=9+AO²-3*AO
AO²-3*AO=4
=>AO=4=>AC=8
=> Из (1) запишем
S(ABCD)=8*6*√3/2/2=12√3
Рассмотрим теперь случай , когда острый угол ВОС. Тогда ∡ВОА=120°
Тогда из ΔАОВ по теореме косинусов запишем:
ВА²=BO²+AO²+2*BO*AO*cos∡BOA
13=9+AO²+3*AO
AO²+3*AO=4
=>AO=1=>AC=2
=> Из (1) запишем
S(ABCD)=2*6*√3/2/2=3√3 см²
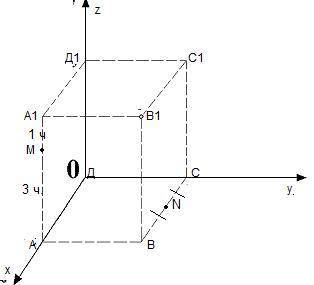
В кубе АА1ВВ1СС1ДД1 точка М лежит на ребре АА1, причем АМ:МА1 = 3:1, а точка N - середина ребра ВС. Найти косинус угла между прямыми: 1.MN и ДД1 2. MN и ВД 3. MN и В1Д 4. MN и А1С
Объяснение:
Введем прямоугольную систему координат.Пусть ребро куба 1.
Тогда координаты точек :
М(1 ;0;0,75) , N(0,5 ;1;0) , Д(0;0;0) ,Д₁(0;0; 1) , В(1;1;0) , В₁(1;1;1) , А₁(1;0;1) , С(0;1;0) .
Найдем координаты векторов
MN(-0,5 ;1; -0,75) , |MN|=√((-0,5)²+1²+(-0,75)²)=0,25√29 ;
ДД₁(0 ;0; 1) , |ДД₁|=√(0²+0²+1²)=1 ;
ВД (-1 ;-1; 0) , |MN|=√((-1)²+(-1)²+0 ²)=√2 ;
В₁Д (-1 ;-1; -1) , |MN|=√3 ;
А₁С(-1 ; 1; -1) , |MN|=√3 ;
Если а(х₁;у₁;z₁) b(х₁;у₁;z₁) ) , то cosα=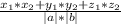 .
.
1) cos(MN ;ДД₁)=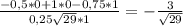 ,
,
2) cos(MN ;ВД)=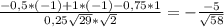 ,
,
3)cos(MN ;В₁Д)=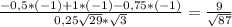 ,
,
4)cos(MN ;А₁С)=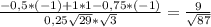 ,
,
S(АВД)=S(АВСД)/2=14.
ВК - медиана в треугольнике АВД, значит S(АВК)=S(КВД)=S(АВД)/2=7
S(КВСД)=S(АВСД)-S(АВК)=28-7=21