
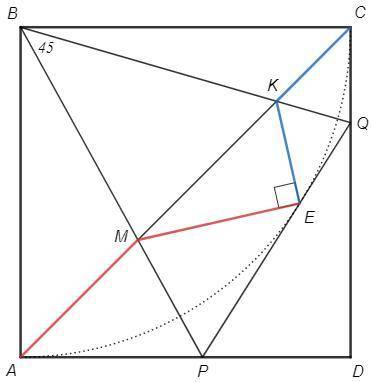
Продлим BM и BK до пересечения со сторонами квадрата в точках P и Q. Рассмотрим треугольник PDQ.
Центр вневписанной окружности треугольника - пересечение биссектрис одного внутреннего и двух внешних углов.
Центр вневписанной окружности лежит на биссектрисе угла D. Отрезок PQ виден из центра вневписанной окружности под углом 90 -D/2. Точка B обладает обоими свойствами, следовательно является центром вневписанной окружности треугольника PDQ.
Пусть E - точка касания вневписанной окружности.
A, C - также точки касания (радиус в точку касания перпендикулярен касательной)
PA=PE, QC=QE (отрезки касательных из одной точки)
PB, QB - биссектрисы
△APM=△EPM, △CQK=△EQK (по двум сторонам и углу между ними)
Следовательно AM=EM, CK=EK
∠MAP=∠MEP=45, ∠KCQ=∠KEQ=45 => ∠MEK=90
ответ:Если две прямые на плоскости,в данный момент это ВК и MN ,перпендикулярны к одной и той же прямой АС,то они параллельны,т к к прямой в плоскости из любой точки можно провести только один перпендикуляр
Параллельность прямых доказана
Теперь об углах
<СМN и <СВК являются соответственными и равны между собой
<СМN=<CBK=46 градусов
В условии сказано,что ВК биссектриса угла АВС
Биссектриса делит угол из которого она проведена на два равных угла,один из них угол СВК
<АВС=<СВК•2=46•2=92 градуса
Объяснение: