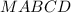- правильная четырехугольная пирамида, около которой описан конус 
⊥ 
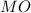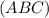
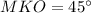
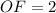см
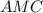- осевое сечение конуса, где 
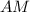и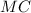 
- образующие конуса
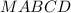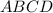
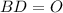
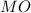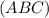
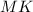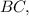- правильная четырехугольная пирамида, 
∩ 
⊥ 
⊥ 
тогда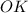 
⊥ 
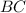и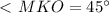 
как линейный угол двугранного угла 
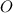- центр окружности, описанной около квадрата 
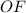, т. е. ⊥ 
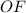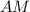
тогда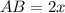 
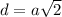, где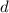 
- диагональ квадрата, 
- сторона квадрата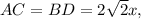
( как диагонали квадрата)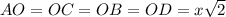
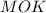- прямоугольный, равнобедренный, следовательно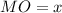 
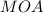- прямоугольный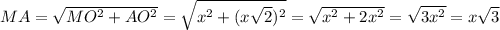
,
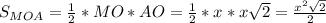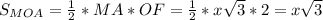
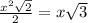
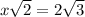
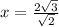
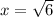
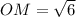см
см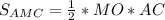
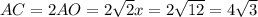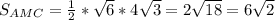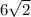(см ²)
см²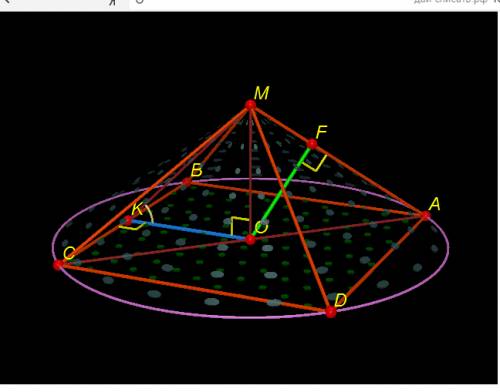
Рисунок сделай сама.
Если назовешь точки касания В и С, то
АО-биссектриса <A, значит делит его пополам. <BAO=<CAO=30
Сторона, лежащая против угла в 30, равна половине гипотенузы. <ABO=90, т.к. опирается на касательную. Значит, ВО=R=AO/2=8/2=4.
ответ:4